Painting Gabriel’s Horn

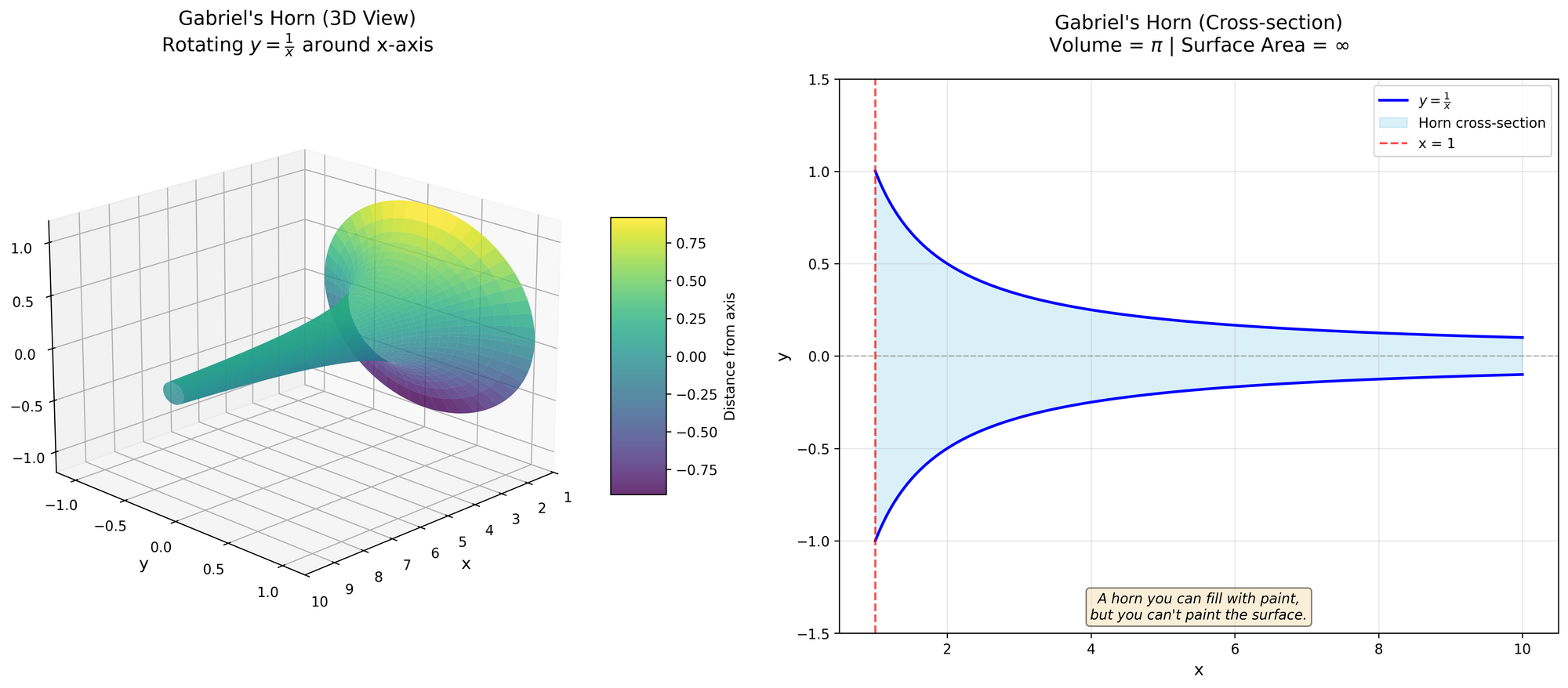
Mathematics is full of wonderful things, but nothing strikes me as more wonderful—or more unintuitive—than Gabriel's Horn.

Here's how it works: take the function $y = \frac{1}{x}$ where $x \in \mathbb{R}^+, 1 \leq x \leq \infty$, and rotate it around the $x$ axis. Not too hard to picture—it looks like a horn. But here's where it gets weird.

Let's calculate the volume. Using solids of revolution, we can show:

$$
V = \pi \lim_{t \rightarrow \infty} \int _1 ^t \frac{1}{x^2} dx = \pi \lim _{t \rightarrow \infty} ( 1 - \frac{1}{t} ) = \pi
$$

Simple, elegant. The volume is exactly $\pi$. Now let's check the surface area.

We know the general definition of arc length is $\int _a ^b \sqrt{1 + f'(x)^2}$. Combining this with our solids of revolution gives us:

$$
A = 2\pi \lim _{t \rightarrow \infty} \int _1 ^t \frac{1}{x} \sqrt{1 + \left( -\frac{1}{x^2} \right)^2 } dx
$$

This integral isn't trivial, but there's a trick. Take the simpler integral $$2\pi \lim _{t \rightarrow \infty} \int _1 ^t \frac{dx}{x}$$ instead. This will always be less than or equal to our original integral (we dropped the $\sqrt{1 + (-\frac{1}{x^2})2}$ term, which is always ≥ 1). Evaluating this simpler integral:

$$
A \geq 2\pi \lim _{t \rightarrow \infty} \int _1 ^t \frac{dx}{x} \implies A \geq \lim _{t \rightarrow \infty} 2\pi \ln(t)
$$

Wait. It diverges. The volume is $V = \pi$, but the surface area is $A \geq \infty$. This isn't a mistake—the math checks out. And that's simply wonderful.

A horn you can fill with paint, but you can't paint the surface.