Markdown Cheatsheet
A comprehensive reference for every Markdown flavor
This guide covers markdown syntax from basic to advanced, across all major flavors. Whether you're writing documentation, blog posts, or technical notes, this reference has you covered.
| Flavor | Best For |
|---|---|
| CommonMark | Universal compatibility |
| GFM | GitHub repos, issues, wikis |
| Pandoc | Academic papers, books |
| Kramdown | Jekyll/Ruby sites |
| MDX | React documentation |
| Obsidian | Personal knowledge bases |
## 1. Basic Syntax (Original Markdown)
### Headings
```markdown
# Heading 1
## Heading 2
### Heading 3
#### Heading 4
##### Heading 5
###### Heading 6
Alternative H1
==============
Alternative H2
--------------
```
### Emphasis
```markdown
*italic* or _italic_
**bold** or __bold__
***bold italic*** or ___bold italic___
~~strikethrough~~ (GFM extension)
```
### Lists
**Unordered:**
```markdown
* Item 1
* Item 2
* Nested item 2.1
* Nested item 2.2
* Deep nested
- Item with dash
+ Item with plus
```
**Ordered:**
```markdown
1. First item
2. Second item
1. Nested ordered
2. Another nested
3. Third item
1. Numbers don't need to be sequential
```
### Links & Images
```markdown
[Inline link](https://example.com "Optional Title")
[Reference link][ref1]
[Implicit reference][]
<https://automatic-link.com>
<email@example.com>

![Reference image][img-ref]
[ref1]: https://example.com "Reference Title"
[Implicit reference]: https://example.com
[img-ref]: image.jpg "Image Reference"
```
### Blockquotes
```markdown
> Single line quote
> Multi-line quote continues here
> and here
> Nested quotes
>> Can be nested
>>> Multiple levels deep
```
### Code
```markdown
Inline `code` with backticks
Code block with 4 spaces
or tab indentation
```
~~~markdown
```
Fenced code block
Multiple lines
```
```javascript
// Syntax highlighted (GFM)
function hello() {
console.log("Hello, World!");
}
```
~~~
### Horizontal Rules
```markdown
Three or more:
---
Hyphens
***
Asterisks
___
Underscores
```
---
## 2. GitHub Flavored Markdown (GFM)
### Tables
```markdown
| Left-aligned | Center-aligned | Right-aligned |
| :----------- | :------------: | ------------: |
| Cell 1 | Cell 2 | Cell 3 |
| Longer text | **Bold** | *Italic* |
Minimal table:
First Header | Second Header
------------ | -------------
Content Cell | Content Cell
```
**Rendered:**
| Left-aligned | Center-aligned | Right-aligned |
| :----------- | :------------: | ------------: |
| Cell 1 | Cell 2 | Cell 3 |
| Longer text | **Bold** | *Italic* |
### Task Lists
```markdown
- [x] Completed task
- [ ] Uncompleted task
- [ ] Another todo
- [x] Nested completed
- [ ] Nested uncompleted
```
**Rendered:**
- [x] Completed task
- [ ] Uncompleted task
- [ ] Another todo
- [x] Nested completed
- [ ] Nested uncompleted
### Username & Issue Mentions
```markdown
@username (GitHub only)
#123 (Issue reference)
user/repo#123 (Cross-repo issue)
```
### Emoji
```markdown
:smile: :heart: :thumbsup: :100:
:rocket: :octocat: :+1: :-1:
```
### Syntax Highlighting with Language
~~~markdown
```python
def factorial(n):
"""Calculate factorial"""
if n <= 1:
return 1
return n * factorial(n - 1)
```
```diff
- Removed line
+ Added line
! Important change
# Comment
```
~~~
**Rendered:**
```python
def factorial(n):
"""Calculate factorial"""
if n <= 1:
return 1
return n * factorial(n - 1)
```
```diff
- Removed line
+ Added line
! Important change
# Comment
```
### SHA References
```markdown
16c999e8c71134401a78d4d46435517b2271d6ac
mojombo@16c999e8c71134401a78d4d46435517b2271d6ac
mojombo/github-flavored-markdown@16c999e
```
---
## 3. CommonMark Extensions
### Autolinks
```markdown
www.example.com (some parsers)
https://example.com
ftp://files.example.com
```
### Disallowed Raw HTML (optional)
```html
<script>alert('This may be stripped');</script>
<div class="custom">Safe HTML allowed in some flavors</div>
```
### Entity & Numeric Character References
```markdown
& < > " '
A A …
```
---
## 4. MultiMarkdown Extensions
### Metadata Block
```markdown
Title: Document Title
Author: John Doe
Date: 2024-01-01
Tags: markdown, reference
Base Header Level: 2
```
### Footnotes
```markdown
Here's a sentence with a footnote[^1].
Here's another with a longer note[^longnote].
Inline footnote^[This is an inline footnote].
[^1]: This is the footnote.
[^longnote]: Here's one with multiple paragraphs.
Indent paragraphs to include them in the footnote.
> Even blockquotes in footnotes!
```
### Citations
```markdown
This is a statement that needs citation[p. 23][#Doe:2024].
Multiple citations[p. 10][#Smith:2023; p. 24][#Doe:2024].
[#Doe:2024]: John Doe. *Sample Book*. 2024.
[#Smith:2023]: Jane Smith. *Another Book*. 2023.
```
### Math (also Pandoc)
```markdown
Inline math: $E = mc^2$ or \\(a^2 + b^2 = c^2\\)
Display math:
$$
\sum_{i=1}^{n} x_i = \int_{0}^{1} f(x) dx
$$
\\[
\frac{-b \pm \sqrt{b^2 - 4ac}}{2a}
\\]
```
### Abbreviations
```markdown
HTML is great.
CSS is awesome.
*[HTML]: HyperText Markup Language
*[CSS]: Cascading Style Sheets
```
### Definition Lists
```markdown
Term 1
: Definition 1
: Another definition
Term 2
: Definition with *inline* **formatting**
Compact Definition
: Brief description
```
### Smart Typography
```markdown
"Smart quotes" and 'single quotes'
En-dash -- and em-dash ---
Ellipsis...
```
### Cross-references
```markdown
See [](#heading-1) for more info.
As discussed in [](#fig:example).
![Example Figure][fig:example]
[fig:example]: image.jpg "Example" width=500px height=300px
```
---
## 5. Pandoc Markdown Extensions
### Div Blocks
```markdown
::: {.note #special-note}
This is a special note block with class and id.
:::
::: warning
This is a warning block.
:::
::: {.sidebar}
Sidebar content here
:::
```
### Span Elements
```markdown
This is [special text]{.highlight #text-id} inline.
[Small caps]{.smallcaps} text.
```
### Line Blocks
```markdown
| The limerick packs laughs anatomical
| In space that is quite economical.
| But the good ones I've seen
| So seldom are clean
| And the clean ones so seldom are comical
```
### Fancy Lists
```markdown
(1) First item
(2) Second item
a. Sub-item
b. Another sub
i. Deep nesting
#. Auto-numbered
#. Continues numbering
i. Roman numerals
ii. Continue
A. Upper letters
B. More items
Example lists:
(@) First example
(@) Second example
Later reference to example (@).
```
### Grid Tables
```markdown
+---------------+---------------+--------------------+
| Fruit | Price | Advantages |
+===============+===============+====================+
| Bananas | $1.34 | - built-in wrapper |
| | | - bright color |
+---------------+---------------+--------------------+
| Oranges | $2.10 | - cures scurvy |
| | | - tasty |
+---------------+---------------+--------------------+
```
### Pipe Tables (simpler)
```markdown
| Right | Left | Default | Center |
|------:|:-----|---------|:------:|
| 12 | 12 | 12 | 12 |
| 123 | 123 | 123 | 123 |
| 1 | 1 | 1 | 1 |
```
### Superscript and Subscript
```markdown
H~2~O is water.
X^2^ is X squared.
^superscript^ and ~subscript~
```
### Inline Code Attributes
```markdown
`code`{.python}
`var x = 5;`{#mycode .javascript .numberLines startFrom="100"}
```
### Raw Blocks
~~~markdown
```{=html}
<div class="custom-html">
Raw HTML preserved exactly
</div>
```
```{=latex}
\begin{align}
E &= mc^2
\end{align}
```
```{=mediawiki}
{{Template|arg=value}}
```
~~~
### YAML Metadata Block
```yaml
---
title: Complete Reference
subtitle: Every Markdown Feature
author:
- name: John Doe
affiliation: University
- name: Jane Smith
date: 2024-01-01
abstract: |
This is a multi-line
abstract in YAML.
tags: [markdown, documentation]
keywords:
- markdown
- reference
lang: en-US
toc: true
toc-depth: 3
numbersections: true
---
```
### Native Spans and Divs
```html
<div custom="attribute">
Native div with attributes
</div>
<span class="custom">Native span</span>
```
---
## 6. Extended Features (Various Flavors)
### Admonitions/Callouts
```markdown
!!! note "Optional Title"
This is a note admonition.
!!! warning
This is a warning without title.
!!! danger "Critical"
Important danger message.
!!! tip
Helpful tip here.
!!! important
Important information.
!!! example "Code Example"
```python
print("Hello")
```
```
**GitHub-style callouts:**
```markdown
> [!NOTE]
> GitHub-style callout
> [!WARNING]
> Another style of callout
> [!TIP]
> Helpful information
> [!IMPORTANT]
> Crucial information
> [!CAUTION]
> Be careful here
```
### Keyboard Keys
```html
Press <kbd>Ctrl</kbd> + <kbd>C</kbd> to copy.
<kbd>⌘</kbd> + <kbd>V</kbd> on Mac.
++ctrl+alt+del++ (some flavors)
```
**Rendered:**
Press <kbd>Ctrl</kbd> + <kbd>C</kbd> to copy.
<kbd>⌘</kbd> + <kbd>V</kbd> on Mac.
### Mark/Highlight
```markdown
==Highlighted text== (some flavors)
<mark>HTML mark element</mark>
{==highlighted==} (critic markup)
```
**Rendered:**
<mark>HTML mark element</mark>
### Insert/Delete (Critic Markup)
```markdown
{++inserted text++}
{--deleted text--}
{~~old~>new~~}
{>>comment<<}
{==highlight==}{>>with comment<<}
```
### Details/Summary
```html
<details>
<summary>Click to expand</summary>
Hidden content here with:
- Lists
- **Formatting**
- Etc.
</details>
<details open>
<summary>Expanded by default</summary>
This is visible initially.
</details>
```
**Rendered:**
<details>
<summary>Click to expand</summary>
Hidden content here with:
- Lists
- **Formatting**
- Etc.
</details>
### Table of Contents
```markdown
[[TOC]] (some flavors)
[TOC] (other flavors)
{:toc} (kramdown)
```
### Include Files
```markdown
<<[file.md]
<<(file.md)
{{file.md}}
!include file.md
{! file.md !}
```
### Diagrams
~~~markdown
```mermaid
graph LR
A[Start] --> B{Decision}
B -->|Yes| C[Do this]
B -->|No| D[Do that]
C --> E[End]
D --> E
```
```plantuml
@startuml
Alice -> Bob: Hello
Bob --> Alice: Hi!
@enduml
```
```graphviz
digraph G {
A -> B;
B -> C;
C -> A;
}
```
~~~
### Custom Containers
```markdown
::: {.theorem #pythagorean}
**Pythagorean Theorem**: $a^2 + b^2 = c^2$
:::
::: note
Custom note container
:::
::: {.callout-note}
## Note Title
Note content
:::
```
### Attributes on Elements
```markdown
{width=50% height=30px}
[Link](url.com){.external target="_blank"}
Paragraph with attributes.
{: .custom-class #custom-id}
```
### Hard Line Breaks
```markdown
Line ending with two spaces
creates a hard break.
Line ending with backslash\
also creates a hard break (some flavors).
```
### Video Embeds (Some Flavors)
```markdown


@[youtube](dQw4w9WgXcQ)
```
### Special Lists
```markdown
Term
~ Definition using tilde
Tight list:
* item1
* item2
Loose list:
* item1
* item2
```
---
## 7. Edge Cases & Special Characters
### Escaping
```markdown
\*Not italic\*
\`Not code\`
\[Not a link\](not a url)
\# Not a heading
\| Not a table
\1. Not a list
```
### Special Characters
```markdown
© ™ ® ° ± ≠ ≤ ≥
→ ← ↑ ↓ ↔
½ ¾ ∞ ∑ ∏
```
**Rendered:**
© ™ ® ° ± ≠ ≤ ≥
→ ← ↑ ↓ ↔
½ ¾ ∞ ∑ ∏
### Zero-Width Characters
```markdown
Zero​Width​Space
Word­Break­Hint
```
### Nested Structures
```markdown
> Blockquote with:
> - List item 1
> - List item 2
> ```python
> # code in list in quote
> print("nested")
> ```
> > Nested quote in list
>
> 1. Ordered in quote
> 2. More ordered
>
> | Table | In | Quote |
> |-------|----|----|
> | Works | In | Some |
```
### Complex Nesting
```markdown
1. List with paragraph
Multiple paragraph in list item.
> Quote in list
```
code in list
```
2. Another item
- [ ] Task in ordered list
- [x] Completed
```
### Unicode & Emoji
```markdown
📝 ✨ 🚀 💻 🎯 ⚡ 🔥 ✅ ❌ ⚠️
α β γ δ ε ζ η θ
© ® ™ • · × ÷ ±
```
### Comments
```markdown
<!-- HTML comment -->
[//]: # (This is also a comment)
[//]: <> (Another comment style)
[comment]: <> (Yet another)
```
---
## 8. Kramdown Specific
### Block Attributes
```markdown
{: .class #id key="value"}
This paragraph has attributes.
> Block quote with attributes.
{: .pullquote}
```
### Options
```markdown
{::options parse_block_html="true" /}
{::options auto_ids="false" /}
```
### No Markdown
```markdown
{::nomarkdown}
This *won't* be **parsed**.
{:/}
```
### Comments
```markdown
{::comment}
This is a kramdown comment.
{:/comment}
```
---
## 9. Markdown Extra
### Special Attributes
```markdown
Header {#header-id .header-class}
================================
[link](url){#link-id .link-class}
```
### Fenced Code Attributes
~~~markdown
~~~ {.python #mycode .numberLines startFrom="10"}
def hello():
print("Hi")
~~~
~~~
### Markdown Inside HTML
```html
<div markdown="1">
This is *markdown* inside **HTML**.
</div>
<div markdown="block">
- List inside HTML
- Another item
</div>
```
### Backslash Escapes
```markdown
\\ \` \* \_ \{ \} \[ \] \( \) \# \+ \- \. \!
```
---
## 10. R Markdown / Quarto
### Code Chunks
~~~markdown
```{r setup, include=FALSE}
knitr::opts_chunk$set(echo = TRUE)
```
```{python}
#| label: fig-plot
#| fig-cap: "Sample Plot"
import matplotlib.pyplot as plt
plt.plot([1, 2, 3], [1, 4, 9])
```
~~~
### Inline R Code
```markdown
The mean is `r mean(c(1,2,3))`.
```
### Chunk Options
~~~markdown
```{r, echo=FALSE, fig.width=6, fig.height=4}
plot(cars)
```
~~~
---
## 11. Wiki-Style Links & Knowledge Base Features
### Wiki Links (Obsidian/Roam/Foam)
```markdown
[[Page Name]]
[[Page Name|Custom Display Text]]
[[Page Name#Heading]]
[[Page Name^block-id]]
![[Embedded Page]]
![[image.png|300x200]]
```
### Block References
```markdown
^unique-block-id
Reference to [[Page#^unique-block-id]]
```
### Tags
```markdown
#tag #multi-word-tag #nested/tag #2024/01/projects
#[[Complex Tag Name]]
```
### Dataview (Obsidian)
~~~markdown
```dataview
TABLE author, rating, finished
FROM #books
WHERE rating > 4
SORT finished DESC
```
`= this.file.name`
`= date(now)`
~~~
---
## 12. MDX (Markdown + JSX)
```jsx
import Button from './Button'
import { Chart } from './Chart'
export const meta = {
title: 'MDX Document',
author: 'John'
}
# {meta.title}
<Button onClick={() => alert('Clicked!')}>
Click me
</Button>
<Chart data={[1, 2, 3]} />
Regular markdown with *React components*.
```
---
## 13. AsciiDoc-Influenced Features
### Admonition Blocks (Alternative Syntax)
```markdown
NOTE: This is a note.
TIP: Helpful tip here.
IMPORTANT: Don't forget this.
WARNING: Be careful!
CAUTION: Critical warning.
```
### Include Directives
```markdown
include::chapter1.md[]
include::code.js[lines=5..10]
```
### Conditional Directives
```markdown
ifdef::env-github[]
This only shows on GitHub.
endif::[]
ifndef::env-github[]
This shows everywhere except GitHub.
endif::[]
```
---
## 14. Mathematical Notation (Extended)
### Display Math Environments
```latex
$$
\begin{align}
a &= b + c \\
d &= e + f + g \\
h &= i
\end{align}
$$
$$
\begin{matrix}
a & b & c \\
d & e & f \\
g & h & i
\end{matrix}
$$
$$
\begin{cases}
x + y = 5 \\
2x - y = 1
\end{cases}
$$
```
### Chemical Equations
```latex
$\ce{2H2 + O2 -> 2H2O}$
$\ce{SO4^2- + Ba^2+ -> BaSO4 v}$
```
### Physics Notation
```latex
$\ket{\psi} = \alpha\ket{0} + \beta\ket{1}$
$\bra{\phi}\ket{\psi}$
```
---
## 15. Diagram Extensions
### PlantUML
~~~markdown
```plantuml
@startuml
!theme plain
actor User
participant "Web Browser" as Browser
participant "Web Server" as Server
database "Database" as DB
User -> Browser: Enter URL
Browser -> Server: HTTP Request
Server -> DB: Query
DB -> Server: Results
Server -> Browser: HTTP Response
Browser -> User: Display Page
@enduml
```
~~~
### Ditaa
~~~markdown
```ditaa
+--------+ +-------+ +-------+
| | --+ ditaa +--> | |
| Text | +-------+ |diagram|
|Document| |!magic!| | |
| {d}| | | | |
+---+----+ +-------+ +-------+
: ^
| Lots of work |
+-------------------------+
```
~~~
### Graphviz DOT
~~~markdown
```dot
digraph finite_state_machine {
rankdir=LR;
size="8,5"
node [shape = doublecircle]; S;
node [shape = point ]; qi
node [shape = circle];
qi -> S;
S -> q1 [ label = "a" ];
S -> S [ label = "a" ];
q1 -> S [ label = "a" ];
q1 -> q2 [ label = "b" ];
q2 -> q1 [ label = "b" ];
q2 -> q2 [ label = "b" ];
}
```
~~~
### Vega-Lite
~~~markdown
```vega-lite
{
"$schema": "https://vega.github.io/schema/vega-lite/v5.json",
"data": {"url": "data.csv"},
"mark": "bar",
"encoding": {
"x": {"field": "category", "type": "nominal"},
"y": {"field": "value", "type": "quantitative"}
}
}
```
~~~
---
## 16. Scholarly Markdown
### Abstract Block
```markdown
{abstract}
This paper presents a comprehensive overview of markdown
flavors and their features. We examine standard syntax
and extended capabilities across implementations.
{/abstract}
```
### Author Block
```markdown
{authors}
John Doe^1^, Jane Smith^2^
^1^ University of Examples
^2^ Institute of Documentation
{/authors}
```
### Keywords
```markdown
{keywords}
markdown, documentation, syntax, reference
{/keywords}
```
### DOI/Bibliography
```markdown
[@doi:10.1000/xyz123] shows that markdown is effective.
See [@smith2024; @doe2023] for more information.
```
### Glossary
```markdown
{glossary}
GFM
: GitHub Flavored Markdown
MMD
: MultiMarkdown
{/glossary}
```
---
## 17. Hugo/Jekyll/Static Site Features
### Front Matter (TOML)
```toml
+++
title = "Post Title"
date = 2024-01-01T10:00:00Z
draft = false
tags = ["markdown", "hugo"]
categories = ["documentation"]
+++
```
### Shortcodes
```markdown
{{</* youtube w7Ft2ymGmfc */>}}
{{</* tweet user="xxx" id="xxx" */>}}
{{</* gist user="xxx" id="xxx" */>}}
{{</* figure src="image.jpg" title="Figure 1" */>}}
{{</* highlight go "linenos=table" */>}}
package main
import "fmt"
func main() {
fmt.Println("Hello")
}
{{</* /highlight */>}}
```
### Jekyll Includes
```liquid
{% include header.html %}
{% include_relative file.md %}
```
### Liquid Templates
```liquid
{% for post in site.posts %}
- [{{ post.title }}]({{ post.url }})
{% endfor %}
{% if page.comments %}
{% include comments.html %}
{% endif %}
```
---
## 18. Markua (LeanPub)
### Aside
```markdown
A> This is an aside (sidebar).
A> It can span multiple lines.
```
### Blurb
```markdown
B> This is a blurb - a textbox with special styling.
```
### Discussion
```markdown
D> This is a discussion box for exercises or questions.
```
### Error/Warning/Information
```markdown
E> This is an error message.
W> This is a warning.
I> This is an information box.
```
### Quiz
```markdown
{quiz, id: quiz1}
? What is 2 + 2?
a) 3
B) 4
c) 5
d) 6
? Which are markdown flavors?
[X] GFM
[X] CommonMark
[ ] XML
[X] Pandoc
{/quiz}
```
---
## 19. Advanced Table Features
### Column Spanning (some flavors)
```markdown
| Column 1 | Column 2 | Column 3 |
|----------|:--------:|---------:|
| span=2 | | Right |
| Left | Center | Right |
```
### MultiMarkdown Tables
```markdown
| | Grouping ||
| First Header | Second Header | Third Header |
| ------------ | :-----------: | -----------: |
| Content | *Long Cell* ||
| Content | **Cell** | Cell |
| New section | More | Data |
| And more | With an escaped '\|' ||
[Table caption, works in MD Extra too]
```
### Grid Table with Alignment
```markdown
+:-----+:-----:+-----:+
| Left |Center |Right |
+======+=======+======+
| L | C | R |
+------+-------+------+
| Left |Center |Right |
+------+-------+------+
```
---
## 20. Custom HTML with Markdown
### Details with Markdown
```html
<details markdown="1">
<summary>Click for markdown content</summary>
- This is a **list**
- With _formatting_
- Inside HTML details
```python
# Even code blocks work
print("Hello from details")
```
</details>
```
### Ruby Annotations
```html
<ruby>
漢字<rt>かんじ</rt>
</ruby>
<ruby>
WWW<rt>World Wide Web</rt>
</ruby>
```
### Progress Bars
```html
<progress value="70" max="100">70%</progress>
<meter value="6" min="0" max="10">6 out of 10</meter>
```
---
## 21. Extended Link Features
### Link Attributes
```markdown
[External Link](https://example.com){:target="_blank" rel="noopener"}
[Download](file.pdf){:download="filename.pdf"}
```
### Anchor Links with IDs
```markdown
{#custom-anchor}
### Heading with Custom ID
Jump to [custom anchor](#custom-anchor)
```
### Protocol Links
```markdown
[Email](mailto:user@example.com?subject=Hello)
[Phone](tel:+1234567890)
[SMS](sms:+1234567890?body=Hello)
[FTP](ftp://files.example.com)
```
---
## 22. Typography Extensions
### Small Caps
```html
<span style="font-variant: small-caps;">Small Caps Text</span>
```
```markdown
%{Small Caps}% (some flavors)
```
### Fractions
```markdown
1/2 1/3 2/3 1/4 3/4 1/8 3/8 5/8 7/8
```
### Ordinals
```markdown
1st 2nd 3rd 4th 21st 42nd
```
### Smart Punctuation
```markdown
"Curly quotes" and 'apostrophes'...
— Em dash and – en dash
(C) (R) (TM) (P) +-
```
---
## 23. Metadata & Processing Instructions
### Processing Instructions
```markdown
{frontmatter}
toc: true
numbered: true
lang: en
{/frontmatter}
{mainmatter}
{backmatter}
```
### Parser Directives
~~~markdown
~~~~~~~~~~~~~~~~~~~~~{.python .numberLines startFrom="100"}
def process():
return "Code with attributes"
~~~~~~~~~~~~~~~~~~~~~
~~~
### Raw LaTeX
```latex
\newpage
\tableofcontents
\listoffigures
\listoftables
```
---
## 24. List Extensions
### Alphabetical Lists
```markdown
a. First item
b. Second item
c. Third item
A. Upper case
B. Continues
C. Through alphabet
```
### Definition Lists (Extended)
```markdown
Apple
: A fruit
: A company
- Makes phones
- Makes computers
: A symbolic object
Orange
Citrus
: Multiple terms, one definition
```
### Interrupted Lists
```markdown
1. First item
<!-- comment breaks list -->
1. New list starts
1. First item
{:.continue}
2. Continues previous list
```
---
## 25. Special Blocks & Environments
### Theorem Environment
```markdown
::: theorem
Let $f$ be a continuous function on $[a,b]$. Then $f$
attains its maximum and minimum values.
:::
::: proof
By the extreme value theorem...
:::
::: lemma
Supporting result here.
:::
::: corollary
Following from the theorem...
:::
```
### Exercise Blocks
```markdown
::: exercise
Prove that $\sqrt{2}$ is irrational.
:::
::: solution
Assume $\sqrt{2} = p/q$ where $p,q$ are integers...
:::
```
---
## 26. Accessibility Features
### Image Descriptions
```markdown
{longdesc="Extended description for screen readers"}
```
### Abbreviation Definitions
```markdown
The HTML specification is maintained by W3C.
*[HTML]: HyperText Markup Language
*[W3C]: World Wide Web Consortium
```
### Language Marking
```html
This is English text. <span lang="es">Esto es español.</span>
<span lang="ja">これは日本語です。</span>
```
---
## 27. Version Control Integration
### Diff Syntax
~~~markdown
```diff
@@ -1,3 +1,3 @@
Line 1
-Line 2 (removed)
+Line 2 (added)
Line 3
```
~~~
### Merge Conflicts
```
<<<<<<< HEAD
Current change
=======
Incoming change
>>>>>>> branch-name
```
### Blame Annotations
```
e83c516 (John 2024-01-01) Initial commit
a4f9b32 (Jane 2024-01-02) Fix typo
```
---
## 28. Additional Special Characters
### Box Drawing
```
┌─────────┬─────────┐
│ Cell 1 │ Cell 2 │
├─────────┼─────────┤
│ Cell 3 │ Cell 4 │
└─────────┴─────────┘
```
### Arrows & Symbols
```
← → ↑ ↓ ↔ ↕ ⇐ ⇒ ⇑ ⇓ ⇔ ⇕
✓ ✗ ✔ ✖ ✚ ★ ☆ ♠ ♣ ♥ ♦
① ② ③ ④ ⑤ ⑥ ⑦ ⑧ ⑨ ⑩
```
### Math Symbols
```
∀ ∃ ∅ ∇ ∈ ∉ ∋ ∏ ∑ ∞
⊂ ⊃ ⊆ ⊇ ∪ ∩ ∧ ∨ ¬ ⊕
```
---
## Summary: Feature Support by Flavor
| Feature | Original | CommonMark | GFM | MMD | Pandoc | Kramdown |
|---------|:--------:|:----------:|:---:|:---:|:------:|:--------:|
| Headings | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ |
| Emphasis | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ |
| Lists | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ |
| Links | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ |
| Images | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ |
| Code blocks | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ |
| Tables | – | – | ✓ | ✓ | ✓ | ✓ |
| Task lists | – | – | ✓ | – | ✓ | – |
| Strikethrough | – | – | ✓ | ✓ | ✓ | ✓ |
| Footnotes | – | – | – | ✓ | ✓ | ✓ |
| Math | – | – | – | ✓ | ✓ | ✓ |
| Definition lists | – | – | – | ✓ | ✓ | ✓ |
| Abbreviations | – | – | – | ✓ | ✓ | ✓ |
| Attributes | – | – | – | ✓ | ✓ | ✓ |
| Div blocks | – | – | – | – | ✓ | – |
| Span elements | – | – | – | – | ✓ | – |
| Superscript | – | – | – | ✓ | ✓ | – |
| Subscript | – | – | – | ✓ | ✓ | – |
---
## Quick Reference Card
| Category | Syntax | Result |
|----------|--------|--------|
| **Headings** | `# H1` `## H2` `### H3` | Heading levels 1-6 |
| **Bold** | `**text**` or `__text__` | **text** |
| **Italic** | `*text*` or `_text_` | *text* |
| **Bold + Italic** | `***text***` | ***text*** |
| **Strikethrough** | `~~text~~` | ~~text~~ |
| **Inline code** | `` `code` `` | `code` |
| **Link** | `[text](url)` | [text](url) |
| **Image** | `` | Embedded image |
| **Blockquote** | `> quote` | Indented quote |
| **Unordered list** | `- item` or `* item` | Bullet list |
| **Ordered list** | `1. item` | Numbered list |
| **Task list** | `- [ ]` / `- [x]` | Checkbox |
| **Horizontal rule** | `---` or `***` | Divider line |
| **Code block** | ` ``` ` or indent 4 spaces | Code block |
| **Table** | `\| col \| col \|` | Table |
| **Footnote** | `[^1]` | Superscript reference |
---
**The golden rule:** Headings, emphasis, lists, links, images, code blocks, and blockquotes work everywhere. Everything else depends on your processor.
1. Basic Syntax (Original Markdown)
Headings
# Heading 1
## Heading 2
### Heading 3
#### Heading 4
##### Heading 5
###### Heading 6
Alternative H1
==============
Alternative H2
--------------
Emphasis
*italic* or _italic_
**bold** or __bold__
***bold italic*** or ___bold italic___
~~strikethrough~~ (GFM extension)
Lists
Unordered:
* Item 1
* Item 2
* Nested item 2.1
* Nested item 2.2
* Deep nested
- Item with dash
+ Item with plus
Ordered:
1. First item
2. Second item
1. Nested ordered
2. Another nested
3. Third item
1. Numbers don't need to be sequential
Links & Images
[Inline link](https://example.com "Optional Title")
[Reference link][ref1]
[Implicit reference][]
<https://automatic-link.com>
<email@example.com>

![Reference image][img-ref]
[ref1]: https://example.com "Reference Title"
[Implicit reference]: https://example.com
[img-ref]: image.jpg "Image Reference"
Blockquotes
> Single line quote
> Multi-line quote continues here
> and here
> Nested quotes
>> Can be nested
>>> Multiple levels deep
Code
Inline `code` with backticks
Code block with 4 spaces
or tab indentation
```
Fenced code block
Multiple lines
```
```javascript
// Syntax highlighted (GFM)
function hello() {
console.log("Hello, World!");
}
```
Horizontal Rules
Three or more:
---
Hyphens
***
Asterisks
___
Underscores
2. GitHub Flavored Markdown (GFM)
Tables
| Left-aligned | Center-aligned | Right-aligned |
| :----------- | :------------: | ------------: |
| Cell 1 | Cell 2 | Cell 3 |
| Longer text | **Bold** | *Italic* |
Minimal table:
First Header | Second Header
------------ | -------------
Content Cell | Content Cell
Rendered:
| Left-aligned | Center-aligned | Right-aligned |
|---|---|---|
| Cell 1 | Cell 2 | Cell 3 |
| Longer text | Bold | Italic |
Task Lists
- [x] Completed task
- [ ] Uncompleted task
- [ ] Another todo
- [x] Nested completed
- [ ] Nested uncompleted
Rendered:
- [x] Completed task
- [ ] Uncompleted task
- [ ] Another todo
- [x] Nested completed
- [ ] Nested uncompleted
Username & Issue Mentions
@username (GitHub only)
#123 (Issue reference)
user/repo#123 (Cross-repo issue)
Emoji
:smile: :heart: :thumbsup: :100:
:rocket: :octocat: :+1: :-1:
Syntax Highlighting with Language
```python
def factorial(n):
"""Calculate factorial"""
if n <= 1:
return 1
return n * factorial(n - 1)
```
```diff
- Removed line
+ Added line
! Important change
# Comment
```
Rendered:
def factorial(n):
"""Calculate factorial"""
if n <= 1:
return 1
return n * factorial(n - 1)
- Removed line
+ Added line
! Important change
# Comment
SHA References
16c999e8c71134401a78d4d46435517b2271d6ac
mojombo@16c999e8c71134401a78d4d46435517b2271d6ac
mojombo/github-flavored-markdown@16c999e
3. CommonMark Extensions
Autolinks
www.example.com (some parsers)
https://example.com
ftp://files.example.com
Disallowed Raw HTML (optional)
<script>alert('This may be stripped');</script>
<div class="custom">Safe HTML allowed in some flavors</div>
Entity & Numeric Character References
& < > " '
A A …
4. MultiMarkdown Extensions
Metadata Block
Title: Document Title
Author: John Doe
Date: 2024-01-01
Tags: markdown, reference
Base Header Level: 2
Footnotes
Here's a sentence with a footnote[^1].
Here's another with a longer note[^longnote].
Inline footnote^[This is an inline footnote].
[^1]: This is the footnote.
[^longnote]: Here's one with multiple paragraphs.
Indent paragraphs to include them in the footnote.
> Even blockquotes in footnotes!
Citations
This is a statement that needs citation[p. 23][#Doe:2024].
Multiple citations[p. 10][#Smith:2023; p. 24][#Doe:2024].
[#Doe:2024]: John Doe. *Sample Book*. 2024.
[#Smith:2023]: Jane Smith. *Another Book*. 2023.
Math (also Pandoc)
Inline math: $E = mc^2$ or \\(a^2 + b^2 = c^2\\)
Display math:
$$
\sum_{i=1}^{n} x_i = \int_{0}^{1} f(x) dx
$$
\\[
\frac{-b \pm \sqrt{b^2 - 4ac}}{2a}
\\]
Abbreviations
HTML is great.
CSS is awesome.
*[HTML]: HyperText Markup Language
*[CSS]: Cascading Style Sheets
Definition Lists
Term 1
: Definition 1
: Another definition
Term 2
: Definition with *inline* **formatting**
Compact Definition
: Brief description
Smart Typography
"Smart quotes" and 'single quotes'
En-dash -- and em-dash ---
Ellipsis...
Cross-references
See [](#heading-1) for more info.
As discussed in [](#fig:example).
![Example Figure][fig:example]
[fig:example]: image.jpg "Example" width=500px height=300px
5. Pandoc Markdown Extensions
Div Blocks
::: {.note #special-note}
This is a special note block with class and id.
:::
::: warning
This is a warning block.
:::
::: {.sidebar}
Sidebar content here
:::
Span Elements
This is [special text]{.highlight #text-id} inline.
[Small caps]{.smallcaps} text.
Line Blocks
| The limerick packs laughs anatomical
| In space that is quite economical.
| But the good ones I've seen
| So seldom are clean
| And the clean ones so seldom are comical
Fancy Lists
(1) First item
(2) Second item
a. Sub-item
b. Another sub
i. Deep nesting
#. Auto-numbered
#. Continues numbering
i. Roman numerals
ii. Continue
A. Upper letters
B. More items
Example lists:
(@) First example
(@) Second example
Later reference to example (@).
Grid Tables
+---------------+---------------+--------------------+
| Fruit | Price | Advantages |
+===============+===============+====================+
| Bananas | $1.34 | - built-in wrapper |
| | | - bright color |
+---------------+---------------+--------------------+
| Oranges | $2.10 | - cures scurvy |
| | | - tasty |
+---------------+---------------+--------------------+
Pipe Tables (simpler)
| Right | Left | Default | Center |
|------:|:-----|---------|:------:|
| 12 | 12 | 12 | 12 |
| 123 | 123 | 123 | 123 |
| 1 | 1 | 1 | 1 |
Superscript and Subscript
H~2~O is water.
X^2^ is X squared.
^superscript^ and ~subscript~
Inline Code Attributes
`code`{.python}
`var x = 5;`{#mycode .javascript .numberLines startFrom="100"}
Raw Blocks
```{=html}
<div class="custom-html">
Raw HTML preserved exactly
</div>
```
```{=latex}
\begin{align}
E &= mc^2
\end{align}
```
```{=mediawiki}
{{Template|arg=value}}
```
YAML Metadata Block
---
title: Complete Reference
subtitle: Every Markdown Feature
author:
- name: John Doe
affiliation: University
- name: Jane Smith
date: 2024-01-01
abstract: |
This is a multi-line
abstract in YAML.
tags: [markdown, documentation]
keywords:
- markdown
- reference
lang: en-US
toc: true
toc-depth: 3
numbersections: true
---
Native Spans and Divs
<div custom="attribute">
Native div with attributes
</div>
<span class="custom">Native span</span>
6. Extended Features (Various Flavors)
Admonitions/Callouts
!!! note "Optional Title"
This is a note admonition.
!!! warning
This is a warning without title.
!!! danger "Critical"
Important danger message.
!!! tip
Helpful tip here.
!!! important
Important information.
!!! example "Code Example"
```python
print("Hello")
```
GitHub-style callouts:
> [!NOTE]
> GitHub-style callout
> [!WARNING]
> Another style of callout
> [!TIP]
> Helpful information
> [!IMPORTANT]
> Crucial information
> [!CAUTION]
> Be careful here
Keyboard Keys
Press <kbd>Ctrl</kbd> + <kbd>C</kbd> to copy.
<kbd>⌘</kbd> + <kbd>V</kbd> on Mac.
++ctrl+alt+del++ (some flavors)
Rendered:
Press Ctrl + C to copy.
⌘ + V on Mac.
Mark/Highlight
==Highlighted text== (some flavors)
<mark>HTML mark element</mark>
{==highlighted==} (critic markup)
Rendered:
HTML mark element
Insert/Delete (Critic Markup)
{++inserted text++}
{--deleted text--}
{~~old~>new~~}
{>>comment<<}
{==highlight==}{>>with comment<<}
Details/Summary
<details>
<summary>Click to expand</summary>
Hidden content here with:
- Lists
- **Formatting**
- Etc.
</details>
<details open>
<summary>Expanded by default</summary>
This is visible initially.
</details>
Rendered:
Click to expand
Hidden content here with:
- Lists
- Formatting
- Etc.
Table of Contents
[[TOC]] (some flavors)
[TOC] (other flavors)
{:toc} (kramdown)
Include Files
<<[file.md]
<<(file.md)
{{file.md}}
!include file.md
{! file.md !}
Diagrams
```mermaid
graph LR
A[Start] --> B{Decision}
B -->|Yes| C[Do this]
B -->|No| D[Do that]
C --> E[End]
D --> E
```
```plantuml
@startuml
Alice -> Bob: Hello
Bob --> Alice: Hi!
@enduml
```
```graphviz
digraph G {
A -> B;
B -> C;
C -> A;
}
```
Custom Containers
::: {.theorem #pythagorean}
**Pythagorean Theorem**: $a^2 + b^2 = c^2$
:::
::: note
Custom note container
:::
::: {.callout-note}
## Note Title
Note content
:::
Attributes on Elements
{width=50% height=30px}
[Link](url.com){.external target="_blank"}
Paragraph with attributes.
{: .custom-class #custom-id}
Hard Line Breaks
Line ending with two spaces
creates a hard break.
Line ending with backslash\
also creates a hard break (some flavors).
Video Embeds (Some Flavors)


@[youtube](dQw4w9WgXcQ)
Special Lists
Term
~ Definition using tilde
Tight list:
* item1
* item2
Loose list:
* item1
* item2
7. Edge Cases & Special Characters
Escaping
\*Not italic\*
\`Not code\`
\[Not a link\](not a url)
\# Not a heading
\| Not a table
\1. Not a list
Special Characters
© ™ ® ° ± ≠ ≤ ≥
→ ← ↑ ↓ ↔
½ ¾ ∞ ∑ ∏
Rendered:
© ™ ® ° ± ≠ ≤ ≥
→ ← ↑ ↓ ↔
½ ¾ ∞ ∑ ∏
Zero-Width Characters
Zero​Width​Space
Word­Break­Hint
Nested Structures
> Blockquote with:
> - List item 1
> - List item 2
> ```python
> # code in list in quote
> print("nested")
> ```
> > Nested quote in list
>
> 1. Ordered in quote
> 2. More ordered
>
> | Table | In | Quote |
> |-------|----|----|
> | Works | In | Some |
Complex Nesting
1. List with paragraph
Multiple paragraph in list item.
> Quote in list
code in list
2. Another item
- [ ] Task in ordered list
- [x] Completed
Unicode & Emoji
📝 ✨ 🚀 💻 🎯 ⚡ 🔥 ✅ ❌ ⚠️
α β γ δ ε ζ η θ
© ® ™ • · × ÷ ±
Comments
<!-- HTML comment -->
[//]: # (This is also a comment)
[//]: <> (Another comment style)
[comment]: <> (Yet another)
8. Kramdown Specific
Block Attributes
{: .class #id key="value"}
This paragraph has attributes.
> Block quote with attributes.
{: .pullquote}
Options
{::options parse_block_html="true" /}
{::options auto_ids="false" /}
No Markdown
{::nomarkdown}
This *won't* be **parsed**.
{:/}
Comments
{::comment}
This is a kramdown comment.
{:/comment}
9. Markdown Extra
Special Attributes
Header {#header-id .header-class}
================================
[link](url){#link-id .link-class}
Fenced Code Attributes
~~~ {.python #mycode .numberLines startFrom="10"}
def hello():
print("Hi")
### Markdown Inside HTML
```html
<div markdown="1">
This is *markdown* inside **HTML**.
</div>
<div markdown="block">
- List inside HTML
- Another item
</div>
```
### Backslash Escapes
```markdown
\\ \` \* \_ \{ \} \[ \] \( \) \# \+ \- \. \!
```
---
## 10. R Markdown / Quarto
### Code Chunks
~~~markdown
```{r setup, include=FALSE}
knitr::opts_chunk$set(echo = TRUE)
```
```{python}
#| label: fig-plot
#| fig-cap: "Sample Plot"
import matplotlib.pyplot as plt
plt.plot([1, 2, 3], [1, 4, 9])
```
Inline R Code
The mean is `r mean(c(1,2,3))`.
Chunk Options
```{r, echo=FALSE, fig.width=6, fig.height=4}
plot(cars)
```
11. Wiki-Style Links & Knowledge Base Features
Wiki Links (Obsidian/Roam/Foam)
[[Page Name]]
[[Page Name|Custom Display Text]]
[[Page Name#Heading]]
[[Page Name^block-id]]
![[Embedded Page]]
![[image.png|300x200]]
Block References
^unique-block-id
Reference to [[Page#^unique-block-id]]
Tags
#tag #multi-word-tag #nested/tag #2024/01/projects
#[[Complex Tag Name]]
Dataview (Obsidian)
```dataview
TABLE author, rating, finished
FROM #books
WHERE rating > 4
SORT finished DESC
```
`= this.file.name`
`= date(now)`
12. MDX (Markdown + JSX)
import Button from './Button'
import { Chart } from './Chart'
export const meta = {
title: 'MDX Document',
author: 'John'
}
# {meta.title}
<Button onClick={() => alert('Clicked!')}>
Click me
</Button>
<Chart data={[1, 2, 3]} />
Regular markdown with *React components*.
13. AsciiDoc-Influenced Features
Admonition Blocks (Alternative Syntax)
NOTE: This is a note.
TIP: Helpful tip here.
IMPORTANT: Don't forget this.
WARNING: Be careful!
CAUTION: Critical warning.
Include Directives
include::chapter1.md[]
include::code.js[lines=5..10]
Conditional Directives
ifdef::env-github[]
This only shows on GitHub.
endif::[]
ifndef::env-github[]
This shows everywhere except GitHub.
endif::[]
14. Mathematical Notation (Extended)
Display Math Environments
$$
\begin{align}
a &= b + c \\
d &= e + f + g \\
h &= i
\end{align}
$$
$$
\begin{matrix}
a & b & c \\
d & e & f \\
g & h & i
\end{matrix}
$$
$$
\begin{cases}
x + y = 5 \\
2x - y = 1
\end{cases}
$$
Chemical Equations
$\ce{2H2 + O2 -> 2H2O}$
$\ce{SO4^2- + Ba^2+ -> BaSO4 v}$
Physics Notation
$\ket{\psi} = \alpha\ket{0} + \beta\ket{1}$
$\bra{\phi}\ket{\psi}$
15. Diagram Extensions
PlantUML
```plantuml
@startuml
!theme plain
actor User
participant "Web Browser" as Browser
participant "Web Server" as Server
database "Database" as DB
User -> Browser: Enter URL
Browser -> Server: HTTP Request
Server -> DB: Query
DB -> Server: Results
Server -> Browser: HTTP Response
Browser -> User: Display Page
@enduml
```
Ditaa
```ditaa
+--------+ +-------+ +-------+
| | --+ ditaa +--> | |
| Text | +-------+ |diagram|
|Document| |!magic!| | |
| {d}| | | | |
+---+----+ +-------+ +-------+
: ^
| Lots of work |
+-------------------------+
```
Graphviz DOT
```dot
digraph finite_state_machine {
rankdir=LR;
size="8,5"
node [shape = doublecircle]; S;
node [shape = point ]; qi
node [shape = circle];
qi -> S;
S -> q1 [ label = "a" ];
S -> S [ label = "a" ];
q1 -> S [ label = "a" ];
q1 -> q2 [ label = "b" ];
q2 -> q1 [ label = "b" ];
q2 -> q2 [ label = "b" ];
}
```
Vega-Lite
```vega-lite
{
"$schema": "https://vega.github.io/schema/vega-lite/v5.json",
"data": {"url": "data.csv"},
"mark": "bar",
"encoding": {
"x": {"field": "category", "type": "nominal"},
"y": {"field": "value", "type": "quantitative"}
}
}
```
16. Scholarly Markdown
Abstract Block
{abstract}
This paper presents a comprehensive overview of markdown
flavors and their features. We examine standard syntax
and extended capabilities across implementations.
{/abstract}
Author Block
{authors}
John Doe^1^, Jane Smith^2^
^1^ University of Examples
^2^ Institute of Documentation
{/authors}
Keywords
{keywords}
markdown, documentation, syntax, reference
{/keywords}
DOI/Bibliography
[@doi:10.1000/xyz123] shows that markdown is effective.
See [@smith2024; @doe2023] for more information.
Glossary
{glossary}
GFM
: GitHub Flavored Markdown
MMD
: MultiMarkdown
{/glossary}
17. Hugo/Jekyll/Static Site Features
Front Matter (TOML)
+++
title = "Post Title"
date = 2024-01-01T10:00:00Z
draft = false
tags = ["markdown", "hugo"]
categories = ["documentation"]
+++
Shortcodes
{{</* youtube w7Ft2ymGmfc */>}}
{{</* tweet user="xxx" id="xxx" */>}}
{{</* gist user="xxx" id="xxx" */>}}
{{</* figure src="image.jpg" title="Figure 1" */>}}
{{</* highlight go "linenos=table" */>}}
package main
import "fmt"
func main() {
fmt.Println("Hello")
}
{{</* /highlight */>}}
Jekyll Includes
{% include header.html %}
{% include_relative file.md %}
Liquid Templates
{% for post in site.posts %}
- [{{ post.title }}]({{ post.url }})
{% endfor %}
{% if page.comments %}
{% include comments.html %}
{% endif %}
18. Markua (LeanPub)
Aside
A> This is an aside (sidebar).
A> It can span multiple lines.
Blurb
B> This is a blurb - a textbox with special styling.
Discussion
D> This is a discussion box for exercises or questions.
Error/Warning/Information
E> This is an error message.
W> This is a warning.
I> This is an information box.
Quiz
{quiz, id: quiz1}
? What is 2 + 2?
a) 3
B) 4
c) 5
d) 6
? Which are markdown flavors?
[X] GFM
[X] CommonMark
[ ] XML
[X] Pandoc
{/quiz}
19. Advanced Table Features
Column Spanning (some flavors)
| Column 1 | Column 2 | Column 3 |
|----------|:--------:|---------:|
| span=2 | | Right |
| Left | Center | Right |
MultiMarkdown Tables
| | Grouping ||
| First Header | Second Header | Third Header |
| ------------ | :-----------: | -----------: |
| Content | *Long Cell* ||
| Content | **Cell** | Cell |
| New section | More | Data |
| And more | With an escaped '\|' ||
[Table caption, works in MD Extra too]
Grid Table with Alignment
+:-----+:-----:+-----:+
| Left |Center |Right |
+======+=======+======+
| L | C | R |
+------+-------+------+
| Left |Center |Right |
+------+-------+------+
20. Custom HTML with Markdown
Details with Markdown
<details markdown="1">
<summary>Click for markdown content</summary>
- This is a **list**
- With _formatting_
- Inside HTML details
```python
# Even code blocks work
print("Hello from details")
Ruby Annotations
<ruby>
漢字<rt>かんじ</rt>
</ruby>
<ruby>
WWW<rt>World Wide Web</rt>
</ruby>
Progress Bars
<progress value="70" max="100">70%</progress>
<meter value="6" min="0" max="10">6 out of 10</meter>
21. Extended Link Features
Link Attributes
[External Link](https://example.com){:target="_blank" rel="noopener"}
[Download](file.pdf){:download="filename.pdf"}
Anchor Links with IDs
{#custom-anchor}
### Heading with Custom ID
Jump to [custom anchor](#custom-anchor)
Protocol Links
[Email](mailto:user@example.com?subject=Hello)
[Phone](tel:+1234567890)
[SMS](sms:+1234567890?body=Hello)
[FTP](ftp://files.example.com)
22. Typography Extensions
Small Caps
<span style="font-variant: small-caps;">Small Caps Text</span>
%{Small Caps}% (some flavors)
Fractions
1/2 1/3 2/3 1/4 3/4 1/8 3/8 5/8 7/8
Ordinals
1st 2nd 3rd 4th 21st 42nd
Smart Punctuation
"Curly quotes" and 'apostrophes'...
— Em dash and – en dash
(C) (R) (TM) (P) +-
23. Metadata & Processing Instructions
Processing Instructions
{frontmatter}
toc: true
numbered: true
lang: en
{/frontmatter}
{mainmatter}
{backmatter}
Parser Directives
~~~~~~~~~~~~~~~~~~~~~{.python .numberLines startFrom="100"}
def process():
return "Code with attributes"
### Raw LaTeX
```latex
\newpage
\tableofcontents
\listoffigures
\listoftables
```
---
## 24. List Extensions
### Alphabetical Lists
```markdown
a. First item
b. Second item
c. Third item
A. Upper case
B. Continues
C. Through alphabet
```
### Definition Lists (Extended)
```markdown
Apple
: A fruit
: A company
- Makes phones
- Makes computers
: A symbolic object
Orange
Citrus
: Multiple terms, one definition
```
### Interrupted Lists
```markdown
1. First item
<!-- comment breaks list -->
1. New list starts
1. First item
{:.continue}
2. Continues previous list
```
---
## 25. Special Blocks & Environments
### Theorem Environment
```markdown
::: theorem
Let $f$ be a continuous function on $[a,b]$. Then $f$
attains its maximum and minimum values.
:::
::: proof
By the extreme value theorem...
:::
::: lemma
Supporting result here.
:::
::: corollary
Following from the theorem...
:::
```
### Exercise Blocks
```markdown
::: exercise
Prove that $\sqrt{2}$ is irrational.
:::
::: solution
Assume $\sqrt{2} = p/q$ where $p,q$ are integers...
:::
```
---
## 26. Accessibility Features
### Image Descriptions
```markdown
{longdesc="Extended description for screen readers"}
```
### Abbreviation Definitions
```markdown
The HTML specification is maintained by W3C.
*[HTML]: HyperText Markup Language
*[W3C]: World Wide Web Consortium
```
### Language Marking
```html
This is English text. <span lang="es">Esto es español.</span>
<span lang="ja">これは日本語です。</span>
```
---
## 27. Version Control Integration
### Diff Syntax
~~~markdown
```diff
@@ -1,3 +1,3 @@
Line 1
-Line 2 (removed)
+Line 2 (added)
Line 3
```
Merge Conflicts
<<<<<<< HEAD
Current change
=======
Incoming change
>>>>>>> branch-name
Blame Annotations
e83c516 (John 2024-01-01) Initial commit
a4f9b32 (Jane 2024-01-02) Fix typo
28. Additional Special Characters
Box Drawing
┌─────────┬─────────┐
│ Cell 1 │ Cell 2 │
├─────────┼─────────┤
│ Cell 3 │ Cell 4 │
└─────────┴─────────┘
Arrows & Symbols
← → ↑ ↓ ↔ ↕ ⇐ ⇒ ⇑ ⇓ ⇔ ⇕
✓ ✗ ✔ ✖ ✚ ★ ☆ ♠ ♣ ♥ ♦
① ② ③ ④ ⑤ ⑥ ⑦ ⑧ ⑨ ⑩
Math Symbols
∀ ∃ ∅ ∇ ∈ ∉ ∋ ∏ ∑ ∞
⊂ ⊃ ⊆ ⊇ ∪ ∩ ∧ ∨ ¬ ⊕
Summary: Feature Support by Flavor
| Feature | Original | CommonMark | GFM | MMD | Pandoc | Kramdown |
|---|---|---|---|---|---|---|
| Headings | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ |
| Emphasis | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ |
| Lists | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ |
| Links | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ |
| Images | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ |
| Code blocks | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ |
| Tables | – | – | ✓ | ✓ | ✓ | ✓ |
| Task lists | – | – | ✓ | – | ✓ | – |
| Strikethrough | – | – | ✓ | ✓ | ✓ | ✓ |
| Footnotes | – | – | – | ✓ | ✓ | ✓ |
| Math | – | – | – | ✓ | ✓ | ✓ |
| Definition lists | – | – | – | ✓ | ✓ | ✓ |
| Abbreviations | – | – | – | ✓ | ✓ | ✓ |
| Attributes | – | – | – | ✓ | ✓ | ✓ |
| Div blocks | – | – | – | – | ✓ | – |
| Span elements | – | – | – | – | ✓ | – |
| Superscript | – | – | – | ✓ | ✓ | – |
| Subscript | – | – | – | ✓ | ✓ | – |
Quick Reference Card
| Category | Syntax | Result |
|---|---|---|
| Headings | # H1 ## H2 ### H3 |
Heading levels 1-6 |
| Bold | **text** or __text__ |
text |
| Italic | *text* or _text_ |
text |
| Bold + Italic | ***text*** |
text |
| Strikethrough | ~~text~~ |
|
| Inline code | `code` |
code |
| Link | [text](url) |
text |
| Image |  |
Embedded image |
| Blockquote | > quote |
Indented quote |
| Unordered list | - item or * item |
Bullet list |
| Ordered list | 1. item |
Numbered list |
| Task list | - [ ] / - [x] |
Checkbox |
| Horizontal rule | --- or *** |
Divider line |
| Code block | ``` or indent 4 spaces |
Code block |
| Table | | col | col | |
Table |
| Footnote | [^1] |
Superscript reference |
The golden rule: Headings, emphasis, lists, links, images, code blocks, and blockquotes work everywhere. Everything else depends on your processor.
TODO
Sorting Algorithms
sort
When I was a Teacher Assistant (TA) in Intro To Computer Science lab, fellow TA
Ian and I were showing off our programming prowess. I thought I had it in the bag: I had solved a competitive programming problem in compile-time (C++ templates are Turing-complete!) and a Space Invaders clone for a class.
But Ian was more clever than I, and showed me something that fundamentally changed how I saw a core-component of programming: a terminal-based (ncurses) sorting algorithm visualizers.
It was the first time I had ever seen these algorithms graphed like this — ever! And, yes, I blame my Algorithm instructor. I finally could see all the hypothetical sorting in a real-life application.
With the power of LLMs in hand, and a website as my canvas, I wanted to see if I could recreate this. Kudos to you, Ian.
Sorting algorithms form the backbone of computer science, serving as fundamental building blocks for countless applications from database management to search engines. This comprehensive guide examines the 25 most important sorting algorithms, organized by type, with detailed analysis of their performance, implementation, and practical applications.
1. Basic Comparison-Based Algorithms
These fundamental algorithms serve as the foundation for understanding sorting concepts, though they generally have O(n²) time complexity.
1.1 Bubble Sort
Complexity Analysis:
- Best Case: O(n) / Ω(n) - when array is already sorted
- Average Case: O(n²) / Θ(n²)
- Worst Case: O(n²)
- Space: O(1)
Properties: Stable, In-place, Adaptive
def bubble_sort(arr):
"""
Bubble Sort with optimization
Time: O(n²) average/worst, O(n) best
Space: O(1)
"""
n = len(arr)
for i in range(n):
swapped = False
# Last i elements are already sorted
for j in range(0, n - i - 1):
if arr[j] > arr[j + 1]:
arr[j], arr[j + 1] = arr[j + 1], arr[j]
swapped = True
# If no swapping occurred, array is sorted
if not swapped:
break
return arr
When to Use:
- Small datasets (< 50 elements)
- Educational purposes - excellent for teaching
- Nearly sorted data
- Memory-constrained environments
Step-by-Step Example:
Array: [64, 34, 25, 12, 22, 11, 90]
Pass 1: [34, 25, 12, 22, 11, 64, 90] - Largest element "bubbles" to end
Pass 2: [25, 12, 22, 11, 34, 64, 90]
... continues until sorted
History: First described by Edward Harry Friend in 1956. The name "bubble sort" was coined by Kenneth E. Iverson due to how smaller elements "bubble" to the top.
Notable Trivia: Donald Knuth famously stated "bubble sort seems to have nothing to recommend it, except a catchy name." Despite criticism, it remains the most taught sorting algorithm due to its simplicity.
1.2 Selection Sort
Complexity Analysis:
- Best/Average/Worst Case: O(n²) - always makes same comparisons
- Space: O(1)
Properties: Unstable, In-place, Not adaptive
def selection_sort(arr):
"""
Selection Sort implementation
Time: O(n²) for all cases
Space: O(1)
"""
n = len(arr)
for i in range(n):
# Find minimum element in remaining unsorted array
min_idx = i
for j in range(i + 1, n):
if arr[j] < arr[min_idx]:
min_idx = j
# Swap the found minimum element
arr[i], arr[min_idx] = arr[min_idx], arr[i]
return arr
When to Use:
- When memory write operations are expensive (e.g., flash memory)
- Small datasets where simplicity matters
- When the number of swaps needs to be minimized
Key Advantage: Performs only O(n) swaps compared to O(n²) for bubble sort.
History: Has ancient origins in manual sorting processes. Formalized in the 1950s as one of the fundamental sorting methods.
1.3 Insertion Sort
Complexity Analysis:
- Best Case: O(n) - already sorted
- Average/Worst Case: O(n²)
- Space: O(1)
Properties: Stable, In-place, Adaptive, Online
def insertion_sort(arr):
"""
Insertion Sort implementation
Time: O(n²) average/worst, O(n) best
Space: O(1)
"""
for i in range(1, len(arr)):
key = arr[i]
j = i - 1
while j >= 0 and arr[j] > key:
arr[j + 1] = arr[j]
j -= 1
arr[j + 1] = key
return arr
When to Use:
- Small datasets (typically < 50 elements)
- Nearly sorted data - performs in O(n) time
- Online algorithms - when data arrives sequentially
- As a subroutine in quicksort and mergesort for small subarrays
Notable Use: Used in Timsort (Python's built-in sort) for small runs. Often faster than O(n log n) algorithms for arrays with fewer than 10-20 elements.
1.4 Shell Sort
Complexity Analysis:
- Best Case: O(n log n)
- Average Case: O(n^1.25) to O(n^1.5) depending on gap sequence
- Worst Case: O(n²) for Shell's original sequence
- Space: O(1)
Properties: Unstable, In-place, Adaptive
def shell_sort(arr):
"""
Shell Sort using Shell's original sequence
Time: O(n²) worst case, O(n log n) average
Space: O(1)
"""
n = len(arr)
gap = n // 2
while gap > 0:
# Perform gapped insertion sort
for i in range(gap, n):
temp = arr[i]
j = i
while j >= gap and arr[j - gap] > temp:
arr[j] = arr[j - gap]
j -= gap
arr[j] = temp
gap //= 2
return arr
When to Use:
- Medium-sized datasets (100-5000 elements)
- When recursion should be avoided
- Embedded systems - simple and efficient
History: Invented by Donald L. Shell in 1959, it was one of the first algorithms to break the O(n²) barrier.
1.5 Cocktail Shaker Sort (Bidirectional Bubble Sort)
Complexity Analysis:
- Best Case: O(n)
- Average/Worst Case: O(n²)
- Space: O(1)
Properties: Stable, In-place, Adaptive, Bidirectional
def cocktail_shaker_sort(arr):
"""
Cocktail Shaker Sort (Bidirectional Bubble Sort)
Time: O(n²) average/worst, O(n) best
Space: O(1)
"""
n = len(arr)
start = 0
end = n - 1
while start < end:
swapped = False
# Forward pass
for i in range(start, end):
if arr[i] > arr[i + 1]:
arr[i], arr[i + 1] = arr[i + 1], arr[i]
swapped = True
if not swapped:
break
end -= 1
swapped = False
# Backward pass
for i in range(end, start, -1):
if arr[i] < arr[i - 1]:
arr[i], arr[i - 1] = arr[i - 1], arr[i]
swapped = True
if not swapped:
break
start += 1
return arr
Advantage: Better than bubble sort at moving small elements (turtles) to the beginning.
2. Efficient Comparison-Based Algorithms
These algorithms achieve O(n log n) average performance and form the backbone of many practical sorting implementations.
2.1 Quick Sort
Complexity Analysis:
- Best/Average Case: O(n log n)
- Worst Case: O(n²) - when pivot is always minimum/maximum
- Space: O(log n) - recursion stack
Properties: Unstable, In-place, Not adaptive
def quicksort(arr, low=0, high=None):
"""
Quicksort with Hoare partition scheme
Time: O(n log n) average, O(n²) worst
Space: O(log n)
"""
if high is None:
high = len(arr) - 1
if low < high:
pivot_idx = partition(arr, low, high)
quicksort(arr, low, pivot_idx)
quicksort(arr, pivot_idx + 1, high)
return arr
def partition(arr, low, high):
"""Hoare partition scheme"""
pivot = arr[low]
i = low - 1
j = high + 1
while True:
i += 1
while arr[i] < pivot:
i += 1
j -= 1
while arr[j] > pivot:
j -= 1
if i >= j:
return j
arr[i], arr[j] = arr[j], arr[i]
Why It's Preferred Despite O(n²) Worst Case:
- Excellent average-case performance with good constant factors
- Cache-friendly sequential access patterns
- In-place sorting
- Modern implementations use introsort to guarantee O(n log n)
History: Invented by Tony Hoare in 1959 while working on machine translation at Moscow State University.
2.2 Merge Sort
Complexity Analysis:
- All Cases: O(n log n) - guaranteed performance
- Space: O(n) - requires additional space for merging
Properties: Stable, Not in-place, Not adaptive
def merge_sort(arr):
"""
Merge Sort implementation
Time: O(n log n) guaranteed
Space: O(n)
"""
if len(arr) <= 1:
return arr
mid = len(arr) // 2
left = merge_sort(arr[:mid])
right = merge_sort(arr[mid:])
return merge(left, right)
def merge(left, right):
"""Merge two sorted arrays"""
result = []
i = j = 0
while i < len(left) and j < len(right):
if left[i] <= right[j]:
result.append(left[i])
i += 1
else:
result.append(right[j])
j += 1
result.extend(left[i:])
result.extend(right[j:])
return result
When to Use:
- When stability is required
- External sorting (large datasets that don't fit in memory)
- Linked lists (efficient with O(1) extra space)
- Parallel processing
History: Invented by John von Neumann in 1945, with detailed analysis published in 1948.
2.3 Heap Sort
Complexity Analysis:
- All Cases: O(n log n) - guaranteed performance
- Space: O(1) - true in-place sorting
Properties: Unstable, In-place, Not adaptive
def heap_sort(arr):
"""
Heap Sort implementation
Time: O(n log n) guaranteed
Space: O(1)
"""
n = len(arr)
# Build max heap
for i in range(n // 2 - 1, -1, -1):
heapify(arr, n, i)
# Extract elements from heap
for i in range(n - 1, 0, -1):
arr[0], arr[i] = arr[i], arr[0]
heapify(arr, i, 0)
return arr
def heapify(arr, n, i):
"""Maintain heap property"""
largest = i
left = 2 * i + 1
right = 2 * i + 2
if left < n and arr[left] > arr[largest]:
largest = left
if right < n and arr[right] > arr[largest]:
largest = right
if largest != i:
arr[i], arr[largest] = arr[largest], arr[i]
heapify(arr, n, largest)
When to Use:
- Memory-constrained environments
- Real-time systems (guaranteed performance)
- Systems concerned with malicious input
History: Invented by J. W. J. Williams in 1964, with in-place version by Robert Floyd.
2.4 Binary Tree Sort
Complexity Analysis:
- Best/Average Case: O(n log n) - with balanced tree
- Worst Case: O(n²) - with unbalanced tree
- Space: O(n) - for tree structure
Properties: Can be stable, Not in-place
When to Use:
- Educational purposes
- When tree structure is needed for other operations
- Online sorting
Note: Self-balancing trees (AVL, Red-Black) guarantee O(n log n) performance.
2.5 Smooth Sort
Complexity Analysis:
- Best Case: O(n) - for sorted data
- Average/Worst Case: O(n log n)
- Space: O(1)
Properties: Unstable, In-place, Adaptive
History: Invented by Edsger W. Dijkstra in 1981 as an improvement over heapsort for partially sorted data.
Notable Use: Used in musl C library's qsort() implementation.
3. Non-Comparison Based Algorithms
These algorithms achieve linear O(n) time complexity by exploiting specific properties of the data rather than comparing elements.
3.1 Counting Sort
Complexity Analysis:
- All Cases: O(n + k) where k is the range of values
- Space: O(n + k)
Properties: Stable, Not in-place
def counting_sort(arr):
"""
Counting Sort for non-negative integers
Time: O(n + k)
Space: O(n + k)
"""
if not arr:
return arr
max_val = max(arr)
count = [0] * (max_val + 1)
# Count occurrences
for num in arr:
count[num] += 1
# Calculate cumulative count
for i in range(1, len(count)):
count[i] += count[i - 1]
# Build output array
output = [0] * len(arr)
for i in range(len(arr) - 1, -1, -1):
output[count[arr[i]] - 1] = arr[i]
count[arr[i]] -= 1
return output
When to Use:
- Sorting integers in a small range
- As a subroutine in radix sort
- When k is O(n) or smaller
History: Invented by Harold H. Seward in 1954 at MIT.
3.2 Radix Sort
Complexity Analysis:
- All Cases: O(d × (n + k)) where d is number of digits
- Space: O(n + k)
Properties:
- LSD (Least Significant Digit): Stable
- MSD (Most Significant Digit): Can be stable
def radix_sort_lsd(arr):
"""
LSD Radix Sort implementation
Time: O(d × (n + k))
Space: O(n + k)
"""
if not arr:
return arr
max_val = max(arr)
exp = 1
while max_val // exp > 0:
counting_sort_for_radix(arr, exp)
exp *= 10
return arr
def counting_sort_for_radix(arr, exp):
n = len(arr)
output = [0] * n
count = [0] * 10
for i in range(n):
index = arr[i] // exp
count[index % 10] += 1
for i in range(1, 10):
count[i] += count[i - 1]
i = n - 1
while i >= 0:
index = arr[i] // exp
output[count[index % 10] - 1] = arr[i]
count[index % 10] -= 1
i -= 1
for i in range(n):
arr[i] = output[i]
When to Use:
- Sorting integers with many digits
- String sorting (MSD variant)
- When d is small compared to log n
History: Dates back to 1887 with Herman Hollerith's tabulating machines.
3.3 Bucket Sort
Complexity Analysis:
- Best/Average Case: O(n + k) for uniform distribution
- Worst Case: O(n²) when all elements fall into one bucket
- Space: O(n + k)
Properties: Stable (if sub-sorting is stable), Not in-place
def bucket_sort(arr):
"""
Bucket Sort for floating-point number
Time: O(n + k) average
Space: O(n + k)
"""
if not arr:
return arr
min_val, max_val = min(arr), max(arr)
bucket_count = len(arr)
buckets = [[] for _ in range(bucket_count)]
# Distribute elements into buckets
for num in arr:
if max_val == min_val:
index = 0
else:
index = int((num - min_val) / (max_val - min_val) * (bucket_count - 1))
buckets[index].append(num)
# Sort individual buckets
result = []
for bucket in buckets:
if bucket:
bucket.sort() # Can use insertion sort
result.extend(bucket)
return result
When to Use:
- Uniformly distributed floating-point numbers
- Large datasets with known range
- When memory is not a constraint
3.4 Pigeonhole Sort
Complexity Analysis:
- All Cases: O(n + range) where range = max - min + 1
- Space: O(range)
Properties: Stable, Not in-place
When to Use:
- Small range of integer values
- When range is comparable to n
- Simple counting applications
History: Based on the pigeonhole principle, formally described by A.J. Lotka (1926).
3.5 Flash Sort
Complexity Analysis:
- Best/Average Case: O(n) for uniform distribution
- Worst Case: O(n²)
- Space: O(m) where m is number of classes
Properties: Unstable, In-place (major advantage)
When to Use:
- Large uniformly distributed datasets
- When memory is limited
- When O(n) average performance is critical
History: Invented by Karl-Dietrich Neubert in 1998 as an efficient in-place implementation of bucket sort.
4. Modern Hybrid Algorithms
These algorithms represent the state-of-the-art in practical sorting, combining multiple techniques for superior performance.
4.1 Timsort
Complexity Analysis:
- Best Case: O(n) - already sorted
- Average/Worst Case: O(n log n)
- Space: O(n)
Properties: Stable, Not in-place
Key Innovations:
- Run Detection: Identifies naturally occurring sorted subsequences
- Minimum Run Size: Calculates optimal minrun (32-64 elements)
- Galloping Mode: Switches to exponential search when one run consistently "wins"
Where It's Used:
- Python's default sort since version 2.3
- Java for sorting objects (Java 7+)
- Android, V8, Swift, Rust
History: Created in 2002 by Tim Peters for Python. A critical bug was discovered and fixed in 2015 through formal verification.
4.2 Introsort (Introspective Sort)
Complexity Analysis:
- All Cases: O(n log n) - guaranteed by heapsort fallback
- Space: O(log n)
Properties: Unstable, In-place
Techniques Combined:
- Quicksort for main sorting
- Heapsort when recursion depth exceeds 2×log₂(n)
- Insertion sort for small subarrays (< 16 elements)
Where It's Used:
- C++ STL's std::sort() in GCC and LLVM
- Microsoft .NET Framework 4.5+
History: Created by David Musser in 1997 to provide guaranteed O(n log n) performance while maintaining quicksort's average-case speed.
4.3 Block Sort (WikiSort)
Complexity Analysis:
- Best Case: O(n)
- Average/Worst Case: O(n log n)
- Space: O(1) - constant space!
Properties: Stable, In-place
Key Innovation: Achieves stable merge sort performance with O(1) space by using internal buffering.
When to Use: When O(1) space complexity and stability are both required.
4.4 Pattern-defeating Quicksort (pdqsort)
Complexity Analysis:
- Best Case: O(n) for specific patterns
- Average/Worst Case: O(n log n)
- Space: O(log n)
Properties: Unstable, In-place
Key Innovations:
- Pattern detection and optimization
- Branchless partitioning
- Adaptive strategy based on input characteristics
Where It's Used:
- Rust's default unstable sort
- C++ Boost libraries
History: Created by Orson Peters in 2016 to improve upon introsort with better pattern handling.
4.5 Dual-Pivot Quicksort
Complexity Analysis:
- Best Case: O(n) when all elements equal
- Average Case: O(n log n) - 5% fewer comparisons than single-pivot
- Worst Case: O(n²) - still possible but less likely
- Space: O(log n)
Properties: Unstable, In-place
Key Innovation: Uses two pivots to partition array into three parts, reducing comparisons.
Where It's Used: Java's default algorithm for primitive arrays since Java 7.
History: Created by Vladimir Yaroslavskiy in 2009, adopted by Java in 2011.
5. Specialized and Educational Algorithms
These algorithms serve specific purposes or demonstrate important concepts in computer science education.
5.1 Comb Sort
Complexity Analysis:
- Best Case: O(n log n)
- Average Case: O(n²/2^p) where p is number of increments
- Worst Case: O(n²)
- Space: O(1)
Properties: Unstable, In-place
Key Feature: Improves upon bubble sort using variable gap with shrink factor of 1.3.
History: Developed by Włodzimierz Dobosiewicz in 1980 to address bubble sort's inefficiency.
5.2 Gnome Sort (Stupid Sort)
Complexity Analysis:
- Best Case: O(n)
- Average/Worst Case: O(n²)
- Space: O(1)
Properties: Stable, In-place, Adaptive
Unique Feature: Uses only a single while loop - inspired by garden gnomes sorting flower pots.
5.3 Cycle Sort
Complexity Analysis:
- All Cases: O(n²)
- Space: O(1)
Properties: Unstable, In-place
Key Feature: Minimizes memory writes - each element is written at most once to its correct position.
When to Use: When memory write operations are expensive (EEPROM, Flash memory).
5.4 Pancake Sort
Complexity Analysis:
- Best Case: O(n)
- Average/Worst Case: O(n²)
- Space: O(1)
Properties: Unstable, In-place
Unique Constraint: Only allowed operation is "flip" (reverse prefix).
Historical Note: Bill Gates' only published academic paper was on this problem (1979), providing a (5n+5)/3 upper bound algorithm.
5.5 Bogo Sort
Complexity Analysis:
- Best Case: O(n) - already sorted
- Average Case: O(n·n!) - expected permutations
- Worst Case: O(∞) - theoretically unbounded
- Space: O(1)
Properties: Unstable, In-place
Educational Value:
- Demonstrates worst-case analysis
- Teaches randomized algorithms
- Shows importance of algorithm selection
import random
def bogo_sort(arr):
"""The worst sorting algorithm ever conceived"""
def is_sorted(arr):
return all(arr[i] <= arr[i+1] for i in range(len(arr)-1))
while not is_sorted(arr):
random.shuffle(arr)
return arr
Trivia: "Quantum Bogo Sort" hypothetically destroys universes where array isn't sorted, leaving only sorted universes.
Summary and Recommendations
Performance Comparison Table
| Algorithm | Best Case | Average Case | Worst Case | Space | Stable | In-Place |
|---|---|---|---|---|---|---|
| Bubble Sort | O(n) | O(n²) | O(n²) | O(1) | Yes | Yes |
| Selection Sort | O(n²) | O(n²) | O(n²) | O(1) | No | Yes |
| Insertion Sort | O(n) | O(n²) | O(n²) | O(1) | Yes | Yes |
| Quick Sort | O(n log n) | O(n log n) | O(n²) | O(log n) | No | Yes |
| Merge Sort | O(n log n) | O(n log n) | O(n log n) | O(n) | Yes | No |
| Heap Sort | O(n log n) | O(n log n) | O(n log n) | O(1) | No | Yes |
| Counting Sort | O(n+k) | O(n+k) | O(n+k) | O(n+k) | Yes | No |
| Radix Sort | O(d(n+k)) | O(d(n+k)) | O(d(n+k)) | O(n+k) | Yes | No |
| Timsort | O(n) | O(n log n) | O(n log n) | O(n) | Yes | No |
When to Use Which Algorithm
For Small Datasets (< 50 elements):
- Insertion Sort - simple and efficient
- Selection Sort - when minimizing swaps matters
For General Purpose:
- Timsort (Python) or Introsort (C++) - best overall performance
- Quick Sort with good pivot selection - excellent average case
For Guaranteed Performance:
- Merge Sort - stable and predictable
- Heap Sort - when O(1) space is required
For Special Data Types:
- Counting Sort - small integer ranges
- Radix Sort - large integers or strings
- Bucket Sort - uniformly distributed floats
For Educational Purposes:
- Start with Bubble Sort for simplicity
- Progress to Quick Sort and Merge Sort
- Use Bogo Sort to demonstrate algorithm analysis
Key Takeaways
- No single best algorithm - choice depends on data characteristics, constraints, and requirements
- Modern algorithms are hybrids - combining techniques yields superior performance
- Stability matters for sorting complex objects where maintaining relative order is important
- Space-time tradeoffs are crucial - some algorithms trade memory for speed
- Real-world performance often differs from theoretical complexity due to cache effects, data patterns, and implementation details
Understanding these 25 algorithms provides a comprehensive foundation for tackling sorting problems in any context, from embedded systems to large-scale data processing.
Dice
Roll With It
Home Row
112 WPM. Take that, typing teacher!
I managed a new high score in TypeRacer today: 112WPM.
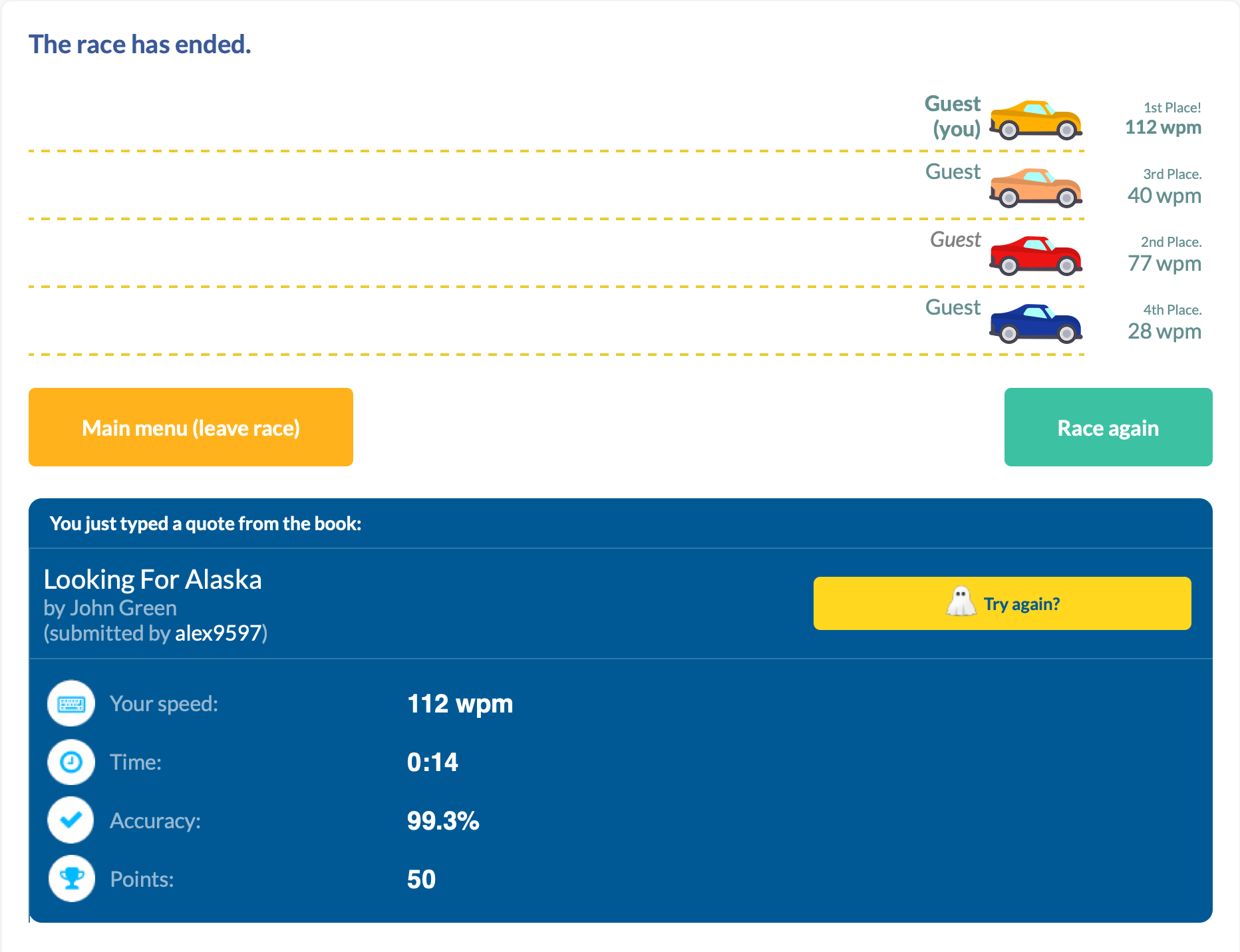
With this article, I wanted to share my journey here, and how I would recommend someone to start.
My Typing Story
I have an interesting history with typing.
I started "typing" at age of five years old to learn the controls of Quake. While the keyboard was a different language with different characters, the muscle memory was the same keyboard-to-keyboard. Upon moving to the states, I changed to an English QWERTY keyboard, and continued playing Doom.
In middle school, before beginning typing class, I clocked in at 35-40 WPM. As I progressed throughout the class, I got familiar with more of the "weird" keys (symbols, numbers, q/z/v) and what a proper "home-row" hand positioning looked like. Midway through the class, I made a discovery about our typing software: you were allowed to make two mistakes, with one word misspell counting as one mistake, and at the end the software took the number of characters you had finished and divided it by 5 (the average word length). So I typed a few words, then held down a random key until the timer expired. And scored 230 WPM.
I thought I was going to get credit for finding a bug our school's software; while my teacher did call my parents that night, it was accuse me of hacking the typing software and changing my score. After explaining to her what I did, her first remedy suggested was a generous failing grade and suspension, but after apologizing to her and the staff, I was only forbidden from being crowned best typist at the school assembly. I may have not gotten an award, but I kept typing skills, reaching 55-65 WPM consistently.
In high school, it was more of the same classes, so I didn't see my typing speed increase drastically—I hovered in the 60-70 WPM range. Even in college, I plateaued around this range.
That is, until I got a mechanical keyboard. I didn't see the results immediately, but with consistent use I bumped my numbers to 65-80 WPM. And this is where I hovered for 5 years; this is where I felt like I had maxed out given the same environment.
I couldn't get any better, because my hand movement prohibited it. While my core fingers mostly stayed in home-row, to achieve my top speed I had developed bad habits to maintain it. Habits such as using right (dominant) index finger to go 3 keys over to the left or using my ring finger in-place of my little finger. While I always returned to home-row, I could feel the excess movement taking its toll, both on my efficiency and general hand strain. During the pandemic, I was working on my computer a lot, and my hands just could not keep up.
So for the first time since I started typing I had to try. It's hard to rewire muscle memory, especially at 30. I tried perfecting every keystroke, getting a massive dopamine hit as I consistently landed the ones I use most often. However, that last 20% feels much harder than the first 20%.
Today, I still try to perfect my craft. I still struggle with my little finger movement. I still catch myself trying to regress some of my old ways when I am trying to compensate and type fast. But today I also typed 112 WPM, and that's cause to celebrate. Take that, typing teacher.
You Too Can Improve
While I can't teach touch typing in a single blog post, I can give a pretty decent summary of it. The following are things I recommend doing in order to become a better typist.
Keyboard
I'll just state it outright: there's no conclusive evidence that ergonomic keyboards actually prevent RSI. Keyboards measurably improve your posture, just not necessarily your health outcomes:
- Alice layouts (Keychron V10, Epomaker Alice) reduce ulnar deviation with 10-degree inward tilt, 2-4 week learning curve
- Fully split keyboards (ErgoDox EZ, ZSA Moonlander) offer maximum adjustability including 0-60 degree tenting, 2-6 weeks to adapt
- Column-staggered designs (Corne, Kyria, Dactyl Manuform) optimize for finger lengths, brutal 1-3 month adaptation
- Kinesis Advantage2 reduces muscle activity in key flexor/extensor muscles, 2 weeks to full mastery
- Traditional ergonomic boards (Microsoft Sculpt, Logitech ERGO K860) offer gentle splits with fixed angles, ~1 month learning curve
- Alternative layouts (Dvorak, Colemak) claim reduced finger travel but have zero clinical trials and 1-3 months of productivity loss
The biomechanical improvements are real and measurable; the clinical benefits remain frustratingly theoretical.
But here's the thing: you don't need empirical evidence on the health benefits if you enjoy typing that much more. Think of it as fun with benefits (FwB, for short...). If you enjoy sitting down at your desk and typing, and it's something you do several hours a day, a keyboard you enjoy could be the push you need to improve other parts of your typing too.
Home Row
Touch typing technique centers on the home row position—ASDF for the left hand and JKL; for the right hand. The F and J keys contain tactile bumps that allow positioning without visual confirmation. This central position minimizes finger travel distance, with proper technique requiring only 0.76-1.5 key distances per character compared to 3.5+ for hunt-and-peck typing.
Each finger has specific responsibilities:
| Hand | Finger | Home Row | Keys Covered |
|---|---|---|---|
| Left | Pinky | A |
Q, A, Z, Tab, Caps Lock, Shift, ` |
| Left | Ring | S |
W, S, X, 2 |
| Left | Middle | D |
E, D, C, 3 |
| Left | Index | F |
R, F, V, T, G, B, 4, 5 |
| Right | Index | J |
Y, H, N, U, J, M, 6, 7 |
| Right | Middle | K |
I, K, ,, 8 |
| Right | Ring | L |
O, L, ., 9 |
| Right | Pinky | ; |
P, ;, /, 0, -, =, [, ], ,, ', Enter, Backspace |
| Both | Thumbs | Space |
Space only |
The index fingers cover the most keys (two columns each), while pinkies cover their column plus all outer keys. After striking any key, fingers must return to home row position—this maintains spatial orientation and prevents positional drift that increases error rates.
Ergonomics
Wrists should remain in neutral position: straight in alignment with forearms, neither bent upward (extension), downward (flexion), nor sideways. During active typing, wrists should float 1-2 inches above the keyboard surface, not resting on the desk or wrist rest. Resting creates contact stress and forces non-neutral positions. Wrist rests serve only for pauses between typing bursts.
Fingers should curve gently, similar to holding a tennis ball. This natural curve allows fingertips to strike keys perpendicularly with optimal mechanical advantage. Palms stay raised above the keyboard while hands maintain this curved posture. The biomechanics of each keystroke involve three distinct muscle activation bursts: extensor muscles lift the finger, flexor muscles drive it downward against keyswitch resistance, and extensors again remove the fingertip. Collision with the end of key travel stops downward motion, not muscle action—meaning excessive force provides no benefit and increases cumulative joint stress.
Arms should hang naturally at the sides with elbows forming 90-110 degree angles. This open angle promotes blood circulation and prevents nerve compression at the elbow. Shoulders remain relaxed and slightly externally rotated, not hunched or rolled forward.
Strength Training
Strength training shows what ergonomic keyboards can't: actual evidence. Research suggests it can significantly reduce injury risk, with clear biological reasons why—it strengthens tendons, improves tissue resilience, and builds endurance in the muscles you use for typing. The formula is simple: use weights or resistance bands (not just bodyweight), train 2-3 times weekly with rest days between, and focus on your forearms, grip, and upper back. Just be patient—tendons adapt slower than muscles, so it takes months to see results.
Conclusion
There's a learning curve to typing. In the beginning you'll see gains with minimal effort, just by knowing roughly where the keys are. As you progress and focus more on your speed, you might sacrifice hand placement (accuracy) for quickly hitting the correct key (speed). As you plateau, it will take more and more focus to correct the muscle memory. And along the way, your typing teacher may try to expel you.
All that matters is fixing your fingers, one key at a time.
iPhone (17?) Air, One Month Later
I fear I am about to feel what iPhone Mini people feel.
I have a confession. After digesting the reviews on iPhone Air, I initially decided to buy iPhone 17 Pro Max instead. This was a luxury upgrade, plain and simple: starry-eyed by the redesign with its bold color (singular—there's only one worth having), I was upgrading from an iPhone 16 Pro Max, using my less-than-full-day battery life (at 99% battery health, no less) as an excuse. But I was a week past the preorder date, and availability for my desired configurations stretched into the weeks-to-months range. So I bought iPhone 17 Air instead in my usual configuration: the newest color, Sky Blue, with 512 GB of storage.
This is my 9th iPhone. My favorite has been iPhone 6 Plus—despite its larger form factor, the comfort factor remains unmatched. No phone since has had that spark; they've been great, just not magical. I kept that phone for three years, my longest streak yet.
I'm happy to pronounce the crown has been passed to iPhone Air.
This phone is every bit as comfortable as phones used to be, but wrapped around 2025 internals. I thought it was time to step down from the Max line because my hands were cramping when I'd use my phone laying down. But I was wrong. It wasn't the size causing problems—it was its close cousin: weight.
Below is a graph of every iPhone's weight. The valleys are base iPhones, the peaks Pro Maxes, color-coded by release year. You'll notice the base iPhone 15 weighs as much as several generations ago's Pro models.
My conclusion: heaviness is here to stay. And that makes me sad. I understand why—customers have been clamoring for less emphasis on thinness and more on the internals: battery, camera, and speakers. To achieve the Air's thinness, Apple had to compromise all three:
- A battery (3,149mAh) that's worse than the base (3,692mAh), Pro (4,252mAh), and Pro Max (5,088mAh)
- A camera with no telephoto or ultra-wide lens
- A speaker that only supports mono sound—they killed the bottom-firing speaker, leaving just the earpiece
On paper, there's no reason to buy an iPhone Air. So why did I keep mine? Am I irrational?
Yes, but hear me out.
Here's the best way I can summarize this phenomenon: My partner has an iPhone 12 Mini. Every time I pick it up, I think "too small for me," and with every clumsy keystroke, I'm certain of it. When I pick up the Pro Max, it demands your full attention: harder to handle without dropping, the weight creates more torque, it commands attention with its imposing presence, and frankly, it's only enjoyable with two hands or resting on something. The Pro line has gotten sharp and unpleasant to hold, like they're designed to be paired with a \$49 case. The base feels hollow and more bulbous than necessary—not cheap, but not premium either.
Then there's iPhone Air. The comfortable phone, regardless of hand size. The big screen you can text on one-handed. The phone in your pocket that doesn't sag your pants™.
It's the first phone I could rock caseless without it getting scratched like hands petting a feral kitten—a habit I sadly had to abandon with iPhone 12 Pro's fragile front glass. This phone made me realize how much I'd bought into the specs and features of the post-iPhone X era, and how little I'd noticed that phones were becoming so uncomfortable I wasn't enjoying using them.
I wanted to give it a month before writing a single word, to ensure I really knew what it was like. I needed to endure all the papercuts: "not being able to pick it up off the table" (super easy unless you put it face down), or "it's so thin it's uncomfortable to hold" (it's the most comfortable phone to hold, period). I needed to experience the missing camera lenses, which usually means repositioning the frame or asking my partner to snap the photo. As an audiophile, I needed acoustic environments where the speakers would falter—turns out that's just roaring showers and noisy kitchens (thanks, AirPods). I needed to feel the pain of terrible battery life, which did require some charger logistics to keep my phone juiced. However, I was already doing this—I haven't had a year-old iPhone that lasts a full day since iPhone 8 (even at 99% battery health). Most online comments say they get the same battery as their iPhone 16 Pros, some even matching Pro Max.
All these trade-offs are worth it, because I finally enjoy using an iPhone for the first time in a long time.
And I'm confident in this because of one piece of anecdotal evidence. Every phone I've handed my partner (iPhones and Pixels), her first words are either "this is heavy" or "this is huge." For the first time in six years, I handed her the Air and she said "wow, this is nice... but I'd put a case on it." That single compliment outweighed every review I'd seen online. I was certain.
The cost of iPhone Air might be too high, but having a phone both you and your partner can use comfortably is priceless.
When I read reviews online, I feel like iPhone Air was dismissed:
- Reviewers and podcasters giving it a day before proclaiming "it's bad and you should feel bad for buying it" as they continue purchasing the same Pro model year after year
- Redditors scoffing at these specs, convinced Apple is doomed
- Hopefuls looking to the future, seeing this as half of next year's foldable
But all these reviewers' subjective opinions are objectively wrong.
First, this phone made me realize I absolutely don't want a foldable. It's the worst of both worlds: insane mass all the time for a book-sized screen you use a fraction of the time. It's not a "foldable," it's a "slablet."
Second, people should blame Apple, not the phone:
- It's awkwardly priced at \$999—\$200 more than the base phone with its complete feature set and just \$100 less than the Pro with everything. This pricing strategy makes zero sense.
- iPhone Air colors are:
whiteSky Blue,whiteLight Gold,whiteCloud White,blackSpace Black. These muted colors position the Air as a sophisticated, minimalist design statement, but this subtle marketing reinforces its role: a niche, aspirational device. - Marketing centers on thinness, not weight and comfort. I thought Apple would've learned from their recent Mac reversal on ultra-thin designs, but apparently not.
- I haven't seen a single Air ad in the wild. Not driving through San Francisco, not on TV, not online. Nowhere except Apple.com, when you scroll past the Pro.
This phone was set up to fail, and I fear in Apple's eyes, it has. It sold so few units that Apple reportedly slashed production volumes drastically. Or not—who knows? What I do know is Apple has a historic precedent for killing the "fourth iPhone slot"—the Minis, Pluses, SEs, and potentially Airs.
I've thought about this phone a lot over the past month—how could I not? It's the most confusing phone in Apple's entire 18-year run. I've realized two things:
- I'll wait for the next iteration (while replacing the battery) unless it takes more than three years—same as my iPhone 6 Plus.
- I'll buy anything Apple releases as the Air's successor. If they add one camera or the other speaker, take my money.
Apple will never be happy with the volumes, and customers will never be happy with their favorite lines being cancelled. So here's my compromise: keep the base iPhone, Pro, and Pro Max unchanged while rotating a different experimental model each year:
- 2025 Air
- 2026 Fold
- 2027 Mini
This is, of course, a thought experiment assuming Apple has infinite money (lol). Creating molds and machinery for single-year iterations would be infeasible. But I dare you to prove me wrong, Mr. Cook.
I fear the iPhone Air is destined for the same graveyard as the Mini—killed by spreadsheets that can't calculate joy and Pro users who mistake weight for value. We'll forever be a tribe of holdouts, nursing ancient technology because Apple forgot how to make things that disappear in your hand instead of demanding attention from it. But maybe that's the price of remembering when phones were toys that delighted us, not digital anchors we're expected to carry.
Solo at Tahoe
1 tent, 13km hike, 1000 calorie breakfasts. No service, no pants, no worries.
This weekend I had the pleasure of camping at William Kent Campground. I'd felt cooped up for a long while, and I needed to clear my head. Taylor and I had originally planned on going together, but we thought it would be more ideal for me to try camping by myself for the first time. We've been going consistently in the cooler months, and I felt more and more confident every time. Was I still nervous? You betcha.
After a day of packing and cooking (with Taylor helping me prep...), I was off. While it usually takes ~3.75 hours to get to Tahoe from our home, it's closer to ~4.25 hours with the Tesla, and in real conditions 4.5-5.5 hours with traffic (if not worse—thanks, Sacramento). I left at a cool 09:30 to arrive by 15:00, making an additional pit stop at a clothing store because my dumbass didn't pack pants. To Tahoe.
I got checked in, had my usual lunch sandwich (and cucumbers with a dab of salt), and then it was onto something much more difficult than driving 4.5 hours: pitching the tent solo. After many failed attempts and several swear words in several languages, it was a beauty. I got the rest of my site set up, and it too was a beauty.






Besides sandwiches, I finally got the pleasure of cooking over the fire with a cast iron skillet—and I must say, this is living. My only complaint about camping was that I eat slow and the food gets cold fast. I don't mind sleeping on the ground in a sleeping bag, I don't mind the lack of showers, I don't even mind the bugs or bears. But hot food is a necessity. I made a big pot of noodles with some spaghetti sauce (thanks Claude the LLM for the recipe and Luigi the human for the hint to use carrots), and created a diabolically good concoction. And it stayed warm for like 30 minutes while I ate in the majesty of nature's grace. For breakfast, I threw eggs, bacon, hash browns, and toast into a skillet and called it good (it was good).





While I was only spending Friday through Sunday, I wanted to make the most of it. I went to bed early for myself (midnight) and woke up quite early (09:00) to get an early rise on the day. I never really touch my phone unless it's for my camera during camping, and this was much of the same. I solely use my Kobo e-reader—this time it was Dragon Ball manga and Game of Thrones: Clash of Kings.
I also managed to get a hike in on the Stanford Rock Trail. Again, my dumbass didn't realize that hiking a bike "rock trail" was going to be rough, but my feet were raw by the time I got back to my site. But I did manage a modest:
- 3h 35m
- 13.42km (8.3mi)
- 1,755 calories
- 1,014ft elevation gain (309m)
- 331 flight of stairs equivalent






On Sunday, I had to depart. After one last 1,000-calorie cast iron breakfast and some time of silence, I was back on the road for home. It's interesting how 70 hours of camping can give you the same sad feelings of leaving as a whole week or two-week vacation. Maybe that's the thing about nature—it doesn't count time in hours or days, but in moments where your mind finally stops racing and you remember what quiet actually sounds like.
📸 Photos are courtesy of iPhone Air.

