Skip to content

Code

latexerr

The most frustrating thing about compiling LaTeX in a terminal is the wall of text that gets written to stdout. An easy solution would be piping to /dev/null—except then you wouldn't be able to get error messages (even if you only pipe stdout to /dev/null and keep stderr). So, I made a solution that handles compiling by piping error messages to less. The syntax latexerr FILENAME will compile the file. Passing --clean will delete temporary LaTeX files.

#!/bin/bash

# USAGE: ./script FILE --clean --glossary

extensions_to_delete=(\
	gz fls fdb_latexmk blg bbl log\
    aux out nav toc snm glg glo xdy
)

compile_and_open() {
    argument="$1"
    auxname="${argument%.tex}.aux"
    errors=$(pdflatex -shell-escape \
        -interaction=nonstopmode \
        -file-line-error "$argument" | \
        grep ".*:[0-9]*:.*")

    if [[ -n $errors ]]; then
        echo "$1 Errors Detected"
        echo "$errors" | less
    else
        open_file $1
        echo "$1 Compile Successful"
    fi
}

open_file() {
    filename=`echo "$1" | cut -d'.' -f1`
    open "$filename.pdf"
    echo "$filename Opened"
}

# http://tex.stackexchange.com/questions/6845/compile-latex-with-bibtex-and-glossaries
glossary() {
    compile $1
    makeglossaries $1
    compile $1
    compile $1
}

clean() {
    for file in $(dirname $1)/*; do
        filename=$(basename "$file")
        extension="${filename##*.}"
        filename="${filename%.*}"

        for bad_extensions in "${extensions_to_delete[@]}" ; do
            if [[ $bad_extensions = $extension ]]; then
                rm $file
                echo "$file Deleted"
            fi
        done
    done
}

main() {
    compile_and_open $1

    if [ "$3" = "--glossary" ]; then
       glossary $1
    fi

    if [ "$2" = "--clean" ]; then
        clean $1
    fi

}

main "$@"
,   &  Illya Starikov
Code

The Monty Hall Problem

The Monty Hall Problem

You've seen it in movies or read about it in books: the Monty Hall Problem. Here's how it works: you're on a game show. There are three doors—behind one is a prize, behind the other two is nothing but disappointment. You pick a door. The host, Monty Hall, opens one of the other doors and reveals there's no prize behind it. Keeping the other two doors closed, he asks if you'd like to switch your choice or stick with your original pick. What should you do? Ben Campbell has a solution.

You mean to tell me that switching mid-game—an offer from the man who set up all the doors and prizes—gives me better odds of winning? How is this possible? Seems a bit counterintuitive. Seems almost wrong. Fortunately, we can test this with a simple program.

import Darwin // for arc4random_uniform

func random(from from: Int, to: Int,
            except: Array<Int>? = nil) -> Int {
    // Produce bounds, +1 to make inclusive
    let number = Int(arc4random_uniform(UInt32(to - from + 1))) + from

    if except != nil && except?.indexOf(number) != nil {
        // Recursively call until we find a valid number
        return random(from: from, to: to, except: except)
    }

    return number
}

// Returns if you won when you stayed and switched, respectively
func montyHall(doors: Int) -> (Bool, Bool) {
    let originalDoor = random(from: 1, to: doors)
    let correctDoor = random(from: 1, to: doors)

    // The door the host reveals
    let revealedDoor = random(from: 1, to: doors,
                              except: [correctDoor, originalDoor])
    // If you switched, this would be your new door
    let switchedDoor = random(from: 1, to: doors,
                              except: [revealedDoor, originalDoor])

    return (originalDoor == correctDoor, switchedDoor == correctDoor)
}

let testValues = [100, 1_000, 10_000, 100_000,
                  1_000_000, 10_000_000]
let actualNumberOfDoors = 3

for value in testValues {
    var stayingCounter = 0, switchingCounter = 0

    for _ in 0...value {
        let (stayedWon, switchedWon) = montyHall(actualNumberOfDoors)
        if stayedWon { stayingCounter += 1 }
        if switchedWon { switchingCounter += 1 }
    }

    let output = "Test Case: \(value). " +
                 "Staying Won: \(stayingCounter), " +
                 "Switching Won: \(switchingCounter)"
    print(output)
}

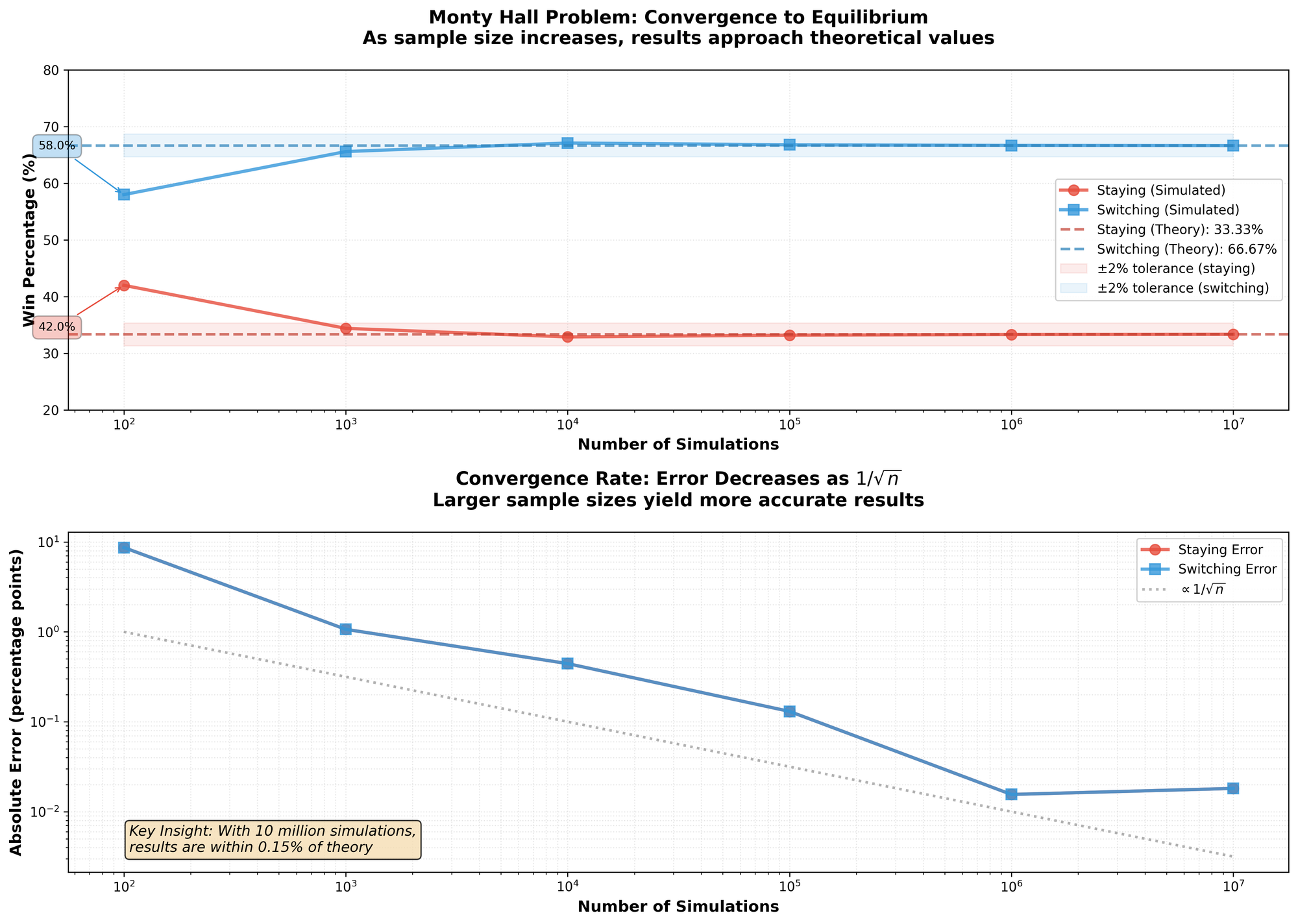
There's no tricks in the code. No gimmicks. So, the results?

Input Staying Won Switching Won
100 42 58
1000 344 656
10000 3289 6711
100000 33203 66797
1000000 333178 666822
10000000 3335146 6664854

It appears that Ben[1] was right. Taking the limit as the input gets higher, switching won roughly $66%$ of the time—compare that to the original $33%$ you got before you were given the option to switch doors. So, how is this possible? I'll explain.

For simplicity, suppose the prize is behind door A out of doors A, B, C. The argument can be made for any initial door, but A makes it easier. At this point, you have a $\frac{1}{3}$ chance of picking the prize no matter what you pick. If you pick door A, the door which contains the prize, the host will definitely want you to change so he will offer you either door B or C. Now suppose you choose a door without the prize, either door B or C. The host has no choice but to eliminate the door without the prize. Meaning if you switch, you have the winning door.

So, why $66%$? Computationally, if you always switch and you picked the wrong door initially, your switch will win every time. There are two incorrect choices out of three, meaning $\frac{2}{3}$ of the time you will win.

You've just had your first lesson in conditional probability.

  1. 21 main character, played by Jim Sturgess ↩︎

,   &  Illya Starikov
Code, Mathematics