Computer Science

Sorting Algorithms

sort(from: bubble, to: Tim)

INITIALIZING...

ALGORITHM

ARRAY SIZE

ARRAY PATTERN

THEME

CUSTOM ARRAY (OPTIONAL)

ANIMATION SPEED 50%

Enter Start

Space Pause

Esc Reset

High array size may impact performance

Select Algorithm

READY TO VISUALIZE

Time: 0.000s

Comparisons: 0

Swaps: 0

WAITING TO START

When I was a Teacher Assistant (TA) in Intro To Computer Science lab, fellow TA
Ian and I were showing off our programming prowess. I thought I had it in the bag: I had solved a competitive programming problem in compile-time (C++ templates are Turing-complete!) and a Space Invaders clone for a class.

But Ian was more clever than I, and showed me something that fundamentally changed how I saw a core-component of programming: a terminal-based (ncurses) sorting algorithm visualizers.
It was the first time I had ever seen these algorithms graphed like this — ever! And, yes, I blame my Algorithm instructor. I finally could see all the hypothetical sorting in a real-life application.

With the power of LLMs in hand, and a website as my canvas, I wanted to see if I could recreate this. Kudos to you, Ian.

Sorting algorithms form the backbone of computer science, serving as fundamental building blocks for countless applications from database management to search engines. This comprehensive guide examines the 25 most important sorting algorithms, organized by type, with detailed analysis of their performance, implementation, and practical applications.

1. Basic Comparison-Based Algorithms

These fundamental algorithms serve as the foundation for understanding sorting concepts, though they generally have O(n²) time complexity.

1.1 Bubble Sort

Complexity Analysis:

Best Case: O(n) / Ω(n) - when array is already sorted
Average Case: O(n²) / Θ(n²)
Worst Case: O(n²)
Space: O(1)

Properties: Stable, In-place, Adaptive

def bubble_sort(arr):
    """
    Bubble Sort with optimization
    Time: O(n²) average/worst, O(n) best
    Space: O(1)
    """
    n = len(arr)

    for i in range(n):
        swapped = False

        # Last i elements are already sorted
        for j in range(0, n - i - 1):
            if arr[j] > arr[j + 1]:
                arr[j], arr[j + 1] = arr[j + 1], arr[j]
                swapped = True

        # If no swapping occurred, array is sorted
        if not swapped:
            break

    return arr

When to Use:

Small datasets (< 50 elements)
Educational purposes - excellent for teaching
Nearly sorted data
Memory-constrained environments

Step-by-Step Example:
Array: [64, 34, 25, 12, 22, 11, 90]

Pass 1: [34, 25, 12, 22, 11, 64, 90] - Largest element "bubbles" to end
Pass 2: [25, 12, 22, 11, 34, 64, 90]
... continues until sorted

History: First described by Edward Harry Friend in 1956. The name "bubble sort" was coined by Kenneth E. Iverson due to how smaller elements "bubble" to the top.

Notable Trivia: Donald Knuth famously stated "bubble sort seems to have nothing to recommend it, except a catchy name." Despite criticism, it remains the most taught sorting algorithm due to its simplicity.

1.2 Selection Sort

Complexity Analysis:

Best/Average/Worst Case: O(n²) - always makes same comparisons
Space: O(1)

Properties: Unstable, In-place, Not adaptive

def selection_sort(arr):
    """
    Selection Sort implementation
    Time: O(n²) for all cases
    Space: O(1)
    """
    n = len(arr)

    for i in range(n):
        # Find minimum element in remaining unsorted array
        min_idx = i

        for j in range(i + 1, n):
            if arr[j] < arr[min_idx]:
                min_idx = j

        # Swap the found minimum element
        arr[i], arr[min_idx] = arr[min_idx], arr[i]

    return arr

When to Use:

When memory write operations are expensive (e.g., flash memory)
Small datasets where simplicity matters
When the number of swaps needs to be minimized

Key Advantage: Performs only O(n) swaps compared to O(n²) for bubble sort.

History: Has ancient origins in manual sorting processes. Formalized in the 1950s as one of the fundamental sorting methods.

1.3 Insertion Sort

Complexity Analysis:

Best Case: O(n) - already sorted
Average/Worst Case: O(n²)
Space: O(1)

Properties: Stable, In-place, Adaptive, Online

def insertion_sort(arr):
    """
    Insertion Sort implementation
    Time: O(n²) average/worst, O(n) best
    Space: O(1)
    """
    for i in range(1, len(arr)):
        key = arr[i]
        j = i - 1

        while j >= 0 and arr[j] > key:
            arr[j + 1] = arr[j]
            j -= 1

        arr[j + 1] = key

    return arr

When to Use:

Small datasets (typically < 50 elements)
Nearly sorted data - performs in O(n) time
Online algorithms - when data arrives sequentially
As a subroutine in quicksort and mergesort for small subarrays

Notable Use: Used in Timsort (Python's built-in sort) for small runs. Often faster than O(n log n) algorithms for arrays with fewer than 10-20 elements.

1.4 Shell Sort

Complexity Analysis:

Best Case: O(n log n)
Average Case: O(n^1.25) to O(n^1.5) depending on gap sequence
Worst Case: O(n²) for Shell's original sequence
Space: O(1)

Properties: Unstable, In-place, Adaptive

def shell_sort(arr):
    """
    Shell Sort using Shell's original sequence
    Time: O(n²) worst case, O(n log n) average
    Space: O(1)
    """
    n = len(arr)
    gap = n // 2

    while gap > 0:
        # Perform gapped insertion sort
        for i in range(gap, n):
            temp = arr[i]
            j = i

            while j >= gap and arr[j - gap] > temp:
                arr[j] = arr[j - gap]
                j -= gap

            arr[j] = temp

        gap //= 2

    return arr

When to Use:

Medium-sized datasets (100-5000 elements)
When recursion should be avoided
Embedded systems - simple and efficient

History: Invented by Donald L. Shell in 1959, it was one of the first algorithms to break the O(n²) barrier.

1.5 Cocktail Shaker Sort (Bidirectional Bubble Sort)

Complexity Analysis:

Best Case: O(n)
Average/Worst Case: O(n²)
Space: O(1)

Properties: Stable, In-place, Adaptive, Bidirectional

def cocktail_shaker_sort(arr):
    """
    Cocktail Shaker Sort (Bidirectional Bubble Sort)
    Time: O(n²) average/worst, O(n) best
    Space: O(1)
    """
    n = len(arr)
    start = 0
    end = n - 1

    while start < end:
        swapped = False

        # Forward pass
        for i in range(start, end):
            if arr[i] > arr[i + 1]:
                arr[i], arr[i + 1] = arr[i + 1], arr[i]
                swapped = True

        if not swapped:
            break

        end -= 1
        swapped = False

        # Backward pass
        for i in range(end, start, -1):
            if arr[i] < arr[i - 1]:
                arr[i], arr[i - 1] = arr[i - 1], arr[i]
                swapped = True

        if not swapped:
            break

        start += 1

    return arr

Advantage: Better than bubble sort at moving small elements (turtles) to the beginning.

2. Efficient Comparison-Based Algorithms

These algorithms achieve O(n log n) average performance and form the backbone of many practical sorting implementations.

2.1 Quick Sort

Complexity Analysis:

Best/Average Case: O(n log n)
Worst Case: O(n²) - when pivot is always minimum/maximum
Space: O(log n) - recursion stack

Properties: Unstable, In-place, Not adaptive

def quicksort(arr, low=0, high=None):
    """
    Quicksort with Hoare partition scheme
    Time: O(n log n) average, O(n²) worst
    Space: O(log n)
    """
    if high is None:
        high = len(arr) - 1

    if low < high:
        pivot_idx = partition(arr, low, high)
        quicksort(arr, low, pivot_idx)
        quicksort(arr, pivot_idx + 1, high)

    return arr

def partition(arr, low, high):
    """Hoare partition scheme"""
    pivot = arr[low]
    i = low - 1
    j = high + 1

    while True:
        i += 1
        while arr[i] < pivot:
            i += 1

        j -= 1
        while arr[j] > pivot:
            j -= 1

        if i >= j:
            return j

        arr[i], arr[j] = arr[j], arr[i]

Why It's Preferred Despite O(n²) Worst Case:

Excellent average-case performance with good constant factors
Cache-friendly sequential access patterns
In-place sorting
Modern implementations use introsort to guarantee O(n log n)

History: Invented by Tony Hoare in 1959 while working on machine translation at Moscow State University.

2.2 Merge Sort

Complexity Analysis:

All Cases: O(n log n) - guaranteed performance
Space: O(n) - requires additional space for merging

Properties: Stable, Not in-place, Not adaptive

def merge_sort(arr):
    """
    Merge Sort implementation
    Time: O(n log n) guaranteed
    Space: O(n)
    """
    if len(arr) <= 1:
        return arr

    mid = len(arr) // 2
    left = merge_sort(arr[:mid])
    right = merge_sort(arr[mid:])

    return merge(left, right)

def merge(left, right):
    """Merge two sorted arrays"""
    result = []
    i = j = 0

    while i < len(left) and j < len(right):
        if left[i] <= right[j]:
            result.append(left[i])
            i += 1
        else:
            result.append(right[j])
            j += 1

    result.extend(left[i:])
    result.extend(right[j:])

    return result

When to Use:

When stability is required
External sorting (large datasets that don't fit in memory)
Linked lists (efficient with O(1) extra space)
Parallel processing

History: Invented by John von Neumann in 1945, with detailed analysis published in 1948.

2.3 Heap Sort

Complexity Analysis:

All Cases: O(n log n) - guaranteed performance
Space: O(1) - true in-place sorting

Properties: Unstable, In-place, Not adaptive

def heap_sort(arr):
    """
    Heap Sort implementation
    Time: O(n log n) guaranteed
    Space: O(1)
    """
    n = len(arr)

    # Build max heap
    for i in range(n // 2 - 1, -1, -1):
        heapify(arr, n, i)

    # Extract elements from heap
    for i in range(n - 1, 0, -1):
        arr[0], arr[i] = arr[i], arr[0]
        heapify(arr, i, 0)

    return arr

def heapify(arr, n, i):
    """Maintain heap property"""
    largest = i
    left = 2 * i + 1
    right = 2 * i + 2

    if left < n and arr[left] > arr[largest]:
        largest = left

    if right < n and arr[right] > arr[largest]:
        largest = right

    if largest != i:
        arr[i], arr[largest] = arr[largest], arr[i]
        heapify(arr, n, largest)

When to Use:

Memory-constrained environments
Real-time systems (guaranteed performance)
Systems concerned with malicious input

History: Invented by J. W. J. Williams in 1964, with in-place version by Robert Floyd.

2.4 Binary Tree Sort

Complexity Analysis:

Best/Average Case: O(n log n) - with balanced tree
Worst Case: O(n²) - with unbalanced tree
Space: O(n) - for tree structure

Properties: Can be stable, Not in-place

When to Use:

Educational purposes
When tree structure is needed for other operations
Online sorting

Note: Self-balancing trees (AVL, Red-Black) guarantee O(n log n) performance.

2.5 Smooth Sort

Complexity Analysis:

Best Case: O(n) - for sorted data
Average/Worst Case: O(n log n)
Space: O(1)

Properties: Unstable, In-place, Adaptive

History: Invented by Edsger W. Dijkstra in 1981 as an improvement over heapsort for partially sorted data.

Notable Use: Used in musl C library's qsort() implementation.

3. Non-Comparison Based Algorithms

These algorithms achieve linear O(n) time complexity by exploiting specific properties of the data rather than comparing elements.

3.1 Counting Sort

Complexity Analysis:

All Cases: O(n + k) where k is the range of values
Space: O(n + k)

Properties: Stable, Not in-place

def counting_sort(arr):
    """
    Counting Sort for non-negative integers
    Time: O(n + k)
    Space: O(n + k)
    """
    if not arr:
        return arr

    max_val = max(arr)
    count = [0] * (max_val + 1)

    # Count occurrences
    for num in arr:
        count[num] += 1

    # Calculate cumulative count
    for i in range(1, len(count)):
        count[i] += count[i - 1]

    # Build output array
    output = [0] * len(arr)
    for i in range(len(arr) - 1, -1, -1):
        output[count[arr[i]] - 1] = arr[i]
        count[arr[i]] -= 1

    return output

When to Use:

Sorting integers in a small range
As a subroutine in radix sort
When k is O(n) or smaller

History: Invented by Harold H. Seward in 1954 at MIT.

3.2 Radix Sort

Complexity Analysis:

All Cases: O(d × (n + k)) where d is number of digits
Space: O(n + k)

Properties:

LSD (Least Significant Digit): Stable
MSD (Most Significant Digit): Can be stable

def radix_sort_lsd(arr):
    """
    LSD Radix Sort implementation
    Time: O(d × (n + k))
    Space: O(n + k)
    """
    if not arr:
        return arr

    max_val = max(arr)
    exp = 1

    while max_val // exp > 0:
        counting_sort_for_radix(arr, exp)
        exp *= 10

    return arr

def counting_sort_for_radix(arr, exp):
    n = len(arr)
    output = [0] * n
    count = [0] * 10

    for i in range(n):
        index = arr[i] // exp
        count[index % 10] += 1

    for i in range(1, 10):
        count[i] += count[i - 1]

    i = n - 1
    while i >= 0:
        index = arr[i] // exp
        output[count[index % 10] - 1] = arr[i]
        count[index % 10] -= 1
        i -= 1

    for i in range(n):
        arr[i] = output[i]

When to Use:

Sorting integers with many digits
String sorting (MSD variant)
When d is small compared to log n

History: Dates back to 1887 with Herman Hollerith's tabulating machines.

3.3 Bucket Sort

Complexity Analysis:

Best/Average Case: O(n + k) for uniform distribution
Worst Case: O(n²) when all elements fall into one bucket
Space: O(n + k)

Properties: Stable (if sub-sorting is stable), Not in-place

def bucket_sort(arr):
    """
    Bucket Sort for floating-point number
    Time: O(n + k) average
    Space: O(n + k)
    """
    if not arr:
        return arr

    min_val, max_val = min(arr), max(arr)
    bucket_count = len(arr)
    buckets = [[] for _ in range(bucket_count)]

    # Distribute elements into buckets
    for num in arr:
        if max_val == min_val:
            index = 0
        else:
            index = int((num - min_val) / (max_val - min_val) * (bucket_count - 1))
        buckets[index].append(num)

    # Sort individual buckets
    result = []
    for bucket in buckets:
        if bucket:
            bucket.sort()  # Can use insertion sort
            result.extend(bucket)

    return result

When to Use:

Uniformly distributed floating-point numbers
Large datasets with known range
When memory is not a constraint

3.4 Pigeonhole Sort

Complexity Analysis:

All Cases: O(n + range) where range = max - min + 1
Space: O(range)

Properties: Stable, Not in-place

When to Use:

Small range of integer values
When range is comparable to n
Simple counting applications

History: Based on the pigeonhole principle, formally described by A.J. Lotka (1926).

3.5 Flash Sort

Complexity Analysis:

Best/Average Case: O(n) for uniform distribution
Worst Case: O(n²)
Space: O(m) where m is number of classes

Properties: Unstable, In-place (major advantage)

When to Use:

Large uniformly distributed datasets
When memory is limited
When O(n) average performance is critical

History: Invented by Karl-Dietrich Neubert in 1998 as an efficient in-place implementation of bucket sort.

4. Modern Hybrid Algorithms

These algorithms represent the state-of-the-art in practical sorting, combining multiple techniques for superior performance.

4.1 Timsort

Complexity Analysis:

Best Case: O(n) - already sorted
Average/Worst Case: O(n log n)
Space: O(n)

Properties: Stable, Not in-place

Key Innovations:

Run Detection: Identifies naturally occurring sorted subsequences
Minimum Run Size: Calculates optimal minrun (32-64 elements)
Galloping Mode: Switches to exponential search when one run consistently "wins"

Where It's Used:

Python's default sort since version 2.3
Java for sorting objects (Java 7+)
Android, V8, Swift, Rust

History: Created in 2002 by Tim Peters for Python. A critical bug was discovered and fixed in 2015 through formal verification.

4.2 Introsort (Introspective Sort)

Complexity Analysis:

All Cases: O(n log n) - guaranteed by heapsort fallback
Space: O(log n)

Properties: Unstable, In-place

Techniques Combined:

Quicksort for main sorting
Heapsort when recursion depth exceeds 2×log₂(n)
Insertion sort for small subarrays (< 16 elements)

Where It's Used:

C++ STL's std::sort() in GCC and LLVM
Microsoft .NET Framework 4.5+

History: Created by David Musser in 1997 to provide guaranteed O(n log n) performance while maintaining quicksort's average-case speed.

4.3 Block Sort (WikiSort)

Complexity Analysis:

Best Case: O(n)
Average/Worst Case: O(n log n)
Space: O(1) - constant space!

Properties: Stable, In-place

Key Innovation: Achieves stable merge sort performance with O(1) space by using internal buffering.

When to Use: When O(1) space complexity and stability are both required.

4.4 Pattern-defeating Quicksort (pdqsort)

Complexity Analysis:

Best Case: O(n) for specific patterns
Average/Worst Case: O(n log n)
Space: O(log n)

Properties: Unstable, In-place

Key Innovations:

Pattern detection and optimization
Branchless partitioning
Adaptive strategy based on input characteristics

Where It's Used:

Rust's default unstable sort
C++ Boost libraries

History: Created by Orson Peters in 2016 to improve upon introsort with better pattern handling.

4.5 Dual-Pivot Quicksort

Complexity Analysis:

Best Case: O(n) when all elements equal
Average Case: O(n log n) - 5% fewer comparisons than single-pivot
Worst Case: O(n²) - still possible but less likely
Space: O(log n)

Properties: Unstable, In-place

Key Innovation: Uses two pivots to partition array into three parts, reducing comparisons.

Where It's Used: Java's default algorithm for primitive arrays since Java 7.

History: Created by Vladimir Yaroslavskiy in 2009, adopted by Java in 2011.

5. Specialized and Educational Algorithms

These algorithms serve specific purposes or demonstrate important concepts in computer science education.

5.1 Comb Sort

Complexity Analysis:

Best Case: O(n log n)
Average Case: O(n²/2^p) where p is number of increments
Worst Case: O(n²)
Space: O(1)

Properties: Unstable, In-place

Key Feature: Improves upon bubble sort using variable gap with shrink factor of 1.3.

History: Developed by Włodzimierz Dobosiewicz in 1980 to address bubble sort's inefficiency.

5.2 Gnome Sort (Stupid Sort)

Complexity Analysis:

Best Case: O(n)
Average/Worst Case: O(n²)
Space: O(1)

Properties: Stable, In-place, Adaptive

Unique Feature: Uses only a single while loop - inspired by garden gnomes sorting flower pots.

5.3 Cycle Sort

Complexity Analysis:

All Cases: O(n²)
Space: O(1)

Properties: Unstable, In-place

Key Feature: Minimizes memory writes - each element is written at most once to its correct position.

When to Use: When memory write operations are expensive (EEPROM, Flash memory).

5.4 Pancake Sort

Complexity Analysis:

Best Case: O(n)
Average/Worst Case: O(n²)
Space: O(1)

Properties: Unstable, In-place

Unique Constraint: Only allowed operation is "flip" (reverse prefix).

Historical Note: Bill Gates' only published academic paper was on this problem (1979), providing a (5n+5)/3 upper bound algorithm.

5.5 Bogo Sort

Complexity Analysis:

Best Case: O(n) - already sorted
Average Case: O(n·n!) - expected permutations
Worst Case: O(∞) - theoretically unbounded
Space: O(1)

Properties: Unstable, In-place

Educational Value:

Demonstrates worst-case analysis
Teaches randomized algorithms
Shows importance of algorithm selection

import random

def bogo_sort(arr):
    """The worst sorting algorithm ever conceived"""
    def is_sorted(arr):
        return all(arr[i] <= arr[i+1] for i in range(len(arr)-1))

    while not is_sorted(arr):
        random.shuffle(arr)

    return arr

Trivia: "Quantum Bogo Sort" hypothetically destroys universes where array isn't sorted, leaving only sorted universes.

Summary and Recommendations

Performance Comparison Table

Algorithm	Best Case	Average Case	Worst Case	Space	Stable	In-Place
Bubble Sort	O(n)	O(n²)	O(n²)	O(1)	Yes	Yes
Selection Sort	O(n²)	O(n²)	O(n²)	O(1)	No	Yes
Insertion Sort	O(n)	O(n²)	O(n²)	O(1)	Yes	Yes
Quick Sort	O(n log n)	O(n log n)	O(n²)	O(log n)	No	Yes
Merge Sort	O(n log n)	O(n log n)	O(n log n)	O(n)	Yes	No
Heap Sort	O(n log n)	O(n log n)	O(n log n)	O(1)	No	Yes
Counting Sort	O(n+k)	O(n+k)	O(n+k)	O(n+k)	Yes	No
Radix Sort	O(d(n+k))	O(d(n+k))	O(d(n+k))	O(n+k)	Yes	No
Timsort	O(n)	O(n log n)	O(n log n)	O(n)	Yes	No

When to Use Which Algorithm

For Small Datasets (< 50 elements):

Insertion Sort - simple and efficient
Selection Sort - when minimizing swaps matters

For General Purpose:

Timsort (Python) or Introsort (C++) - best overall performance
Quick Sort with good pivot selection - excellent average case

For Guaranteed Performance:

Merge Sort - stable and predictable
Heap Sort - when O(1) space is required

For Special Data Types:

Counting Sort - small integer ranges
Radix Sort - large integers or strings
Bucket Sort - uniformly distributed floats

For Educational Purposes:

Start with Bubble Sort for simplicity
Progress to Quick Sort and Merge Sort
Use Bogo Sort to demonstrate algorithm analysis

Key Takeaways

No single best algorithm - choice depends on data characteristics, constraints, and requirements
Modern algorithms are hybrids - combining techniques yields superior performance
Stability matters for sorting complex objects where maintaining relative order is important
Space-time tradeoffs are crucial - some algorithms trade memory for speed
Real-world performance often differs from theoretical complexity due to cache effects, data patterns, and implementation details

Understanding these 25 algorithms provides a comprehensive foundation for tackling sorting problems in any context, from embedded systems to large-scale data processing.

Saturday, 22 November 2025

, & Illya Starikov

Computer Science, Code

Evolutionary Algorithms Endgame Dynamics

Adaptive Restarts and Termination Conditions

Update: Previously, a system was introduced for detecting if an individual was stuck at a local optimum. After extensive testing, this system was shown to be fragile. This post has been updated to showcase a more robust system.

Previously our Evolutionary Algorithms had it pretty easy: there would be either one local optimum (like our Secret Message problem instance) or multiple valid local optima (like the 3-SAT problem instance). In the real world, we might not be so lucky.

Often, an Evolutionary Algorithm might encounter a local optimum within the search space, and it will not be so easy to escape — offspring generated will be in close proximity of the optimum, and the mutation will not be enough to start exploring other parts of the search space.

To add to the frustration, there might not enough time or patience to wait for the Evolutionary Algorithm to finish. We might have different criteria we are looking for, outside of just a fitness target.

We are going to tackle both of these issues.

Applying Termination Conditions

First, we will examine what criteria we want met before our Evolutionary Algorithm terminates. In general, there are six that are universal:

Date and Time. After a specified date and time, terminate.
Fitness Target. This is what we had before; terminate when any individual attains a certain fitness.
Number of Fitness Evaluations. Every generation, every individual's fitness is evaluated (in our case, every generation $\mu + \lambda$ fitnesses are evaluated). Terminate after a specified number of fitness evaluations.
Number of Generations. Just like the number of fitness evaluations, terminate after a specified generations.
No Change In Average Fitness. This is a bit tricky. After specify $N$ generations, we check every $N$ generations back to determine if the average fitness of a population has improved. We have to be careful in our programming; by preserving diversity, we almost always lose fitness.
No Change In Best Fitness. Just like No Change In Average Fitness, but instead of taking the average fitness, we take the best.

Later, we will see how Conditions 5 & 6 will come in handy to determining if we are stuck in a local optimum.

To make sure we are always given valid termination conditions, we will have a super class that all termination conditions will inherit from. From there, we will have a separate condition for each of the listed conditions above.

class _TerminationCondition:
    pass

class FitnessTarget(_TerminationCondition):
    """Terminate after an individual reaches a particular fitness."""

class DateTarget(_TerminationCondition):
    """Terminate after a particular date and time."""

class NoChangeInAverageFitness(_TerminationCondition):
    """Terminate after there has been no change in the average
    fitness for a period of time."""

class NoChangeInBestFitness(_TerminationCondition):
    """Terminate after there has been no change in the best fitness
    for a period of time."""

class NumberOfFitnessEvaluations(_TerminationCondition):
    """Terminate after a particular number of fitness evaluations."""

class NumberOfGenerations(_TerminationCondition):
    """Terminate after a particular number of generations."""

Now, we need something that will keep track of all these conditions, and tells us when we should terminate. And here's where we need to be careful.

First, we need to know when to terminate. We want to mix and match different conditions, depending on the use case. This begs the questions:

Should the Evolutionary Algorithm terminate when one condition has been met, or all of them?

Generally, it makes more sense to terminate when any of the conditions have been met, as opposed to all of them. Suppose the two termination conditions are date and target fitness. It does not make sense to keep going after the target fitness is reached, and (if in a time crunch) it does not make sense to keep going after a specified date.

Second, how should we define no change in average/best fitness? These values can be quite sinusoidal, so we want to be more conservative in our definition. One plausible solution is to take the average of the first quartile (the first 25% to ever enter the queue), and see if the there is a single individual with a better fitness in the second, third, or fourth quartile (the last 75% percent to enter the queue). This way, even if there were very dominant individuals in the beginning, a single, more dominant individual will continue the Evolutionary Algorithm.

From this, we have everything we might need to keep track of our terminating conditions.

class TerminationManager:
    def __init__(self, termination_conditions, fitness_selector):
        assert isinstance(termination_conditions, list)
        assert all(issubclass(type(condition), _TerminationCondition)
                   for condition in termination_conditions), \
               "Termination condition is not valid"

        self.termination_conditions = termination_conditions
        self.__fitness_selector = fitness_selector

        self.__best_fitnesses = []
        self.__average_fitnesses = []

        self.__number_of_fitness_evaluations = 0
        self.__number_of_generations = 0

    def should_terminate(self):
        for condition in self.termination_conditions:
            if (isinstance(condition, FitnessTarget) and
                    self.__fitness_should_terminate()):
                return True
            elif (isinstance(condition, DateTarget) and
                    self.__date_should_terminate()):
                return True
            elif (isinstance(condition, NoChangeInAverageFitness) and
                    self.__average_fitness_should_terminate()):
                return True
            elif (isinstance(condition, NoChangeInBestFitness) and
                    self.__best_fitness_should_terminate()):
                return True
            elif (isinstance(condition, NumberOfFitnessEvaluations) and
                    self.__fitness_evaluations_should_terminate()):
                return True
            elif (isinstance(condition, NumberOfGenerations) and
                    self.__generations_should_terminate()):
                return True

        return False

    def reset(self):
        """Reset the best fitnesses, average fitnesses, number of
        generations, and number of fitness evaluations."""
        self.__best_fitnesses = []
        self.__average_fitnesses = []

        self.__number_of_fitness_evaluations = 0
        self.__number_of_generations = 0

    def __fitness_should_terminate(self):
        """Determine if should terminate based on the max fitness."""

    def __date_should_terminate(self):
        """Determine if should terminate based on the date."""

    def __average_fitness_should_terminate(self):
        """Determine if should terminate based on the average fitness
        for the last N generations."""

    def __best_fitness_should_terminate(self):
        """Determine if should terminate based on the average fitness
        for the last N generations."""

    def __fitness_evaluations_should_terminate(self):
        """Determine if should terminate based on the number of
        fitness evaluations."""

    def __generations_should_terminate(self):
        """Determine if should terminate based on the number of generations."""

And the changes to our Evolutionary Algorithm are minimal, too.

class EA:
    ...
    
    def search(self, termination_conditions):
        generation = 1
        self.population = Population(self.μ, self.λ)

        fitness_getter = lambda: [individual.fitness
                                  for individual
                                  in self.population.individuals]
        termination_manager = TerminationManager(termination_conditions,
                                                  fitness_getter)

        while not termination_manager.should_terminate():
            offspring = Population.generate_offspring(self.population)
            self.population.individuals += offspring.individuals
            self.population = Population.survival_selection(
                self.population)

            print("Generation #{}: {}".format(
                generation, self.population.fittest.fitness))
            generation += 1

        print("Result: {}".format(self.population.fittest.genotype))
        return self.population.fittest

However, we can still do better.

Generations Into Epochs

Before, the Evolutionary Algorithm framework we put in place was strictly a generational model. One generation lead to the next, and there were no discontinuities. Now, let's make our generational model into an epochal one.

We define an epoch as anytime our Evolutionary Algorithm encounters a local optimum. Once the end of an epoch is reached, the EA is reset, and the previous epoch is saved. Upon approaching the end of the next epoch, reintroduce the last epoch into the population; by this, more of the search space is covered.

How can we determine if we are at a local optimum?

We can't.

That does not mean we cannot have a heuristic for it. When there is little to no change in average/best fitness for a prolonged period of time, that typically means a local optimum has been reached. How long is a prolonged period of time? That's undetermined; it is another parameter we have to account for.

Note, if the Evolutionary Algorithm keeps producing more fit individuals, but the average fitness remains the same, the algorithm will terminate. Likewise, if the best fitness remains the same, but the average fitness closely approaches the best, the EA will terminate. Therefore, we should determine if the best fitness and the average fitness has not changed; only then should we start a new epoch.

Luckily, we already have something that will manage the average/best fitness for us.

class EA:
    ...

    def search(self, termination_conditions):
        epochs, generation, total_generations = 1, 1, 1
        self.population = Population(self.μ, self.λ)

        previous_epoch = []
        fitness_getter = lambda: [individual.fitness
                                  for individual
                                  in self.population.individuals]

        termination_manager = TerminationManager(termination_conditions,
                                                  fitness_getter)
        epoch_manager_best_fitness = TerminationManager(
            [NoChangeInBestFitness(250)], fitness_getter)
        epoch_manager_average_fitness = TerminationManager(
            [NoChangeInAverageFitness(250)], fitness_getter)

        while not termination_manager.should_terminate():
            if (epoch_manager_best_fitness.should_terminate() and
                    epoch_manager_average_fitness.should_terminate()):
                if len(previous_epoch) > 0:
                    epoch_manager_best_fitness.reset()
                    epoch_manager_average_fitness.reset()

                    self.population.individuals += previous_epoch
                    previous_epoch = []
                else:
                    epoch_manager_best_fitness.reset()
                    epoch_manager_average_fitness.reset()

                    previous_epoch = self.population.individuals
                    self.population = Population(self.μ, self.λ)

                    generation = 0
                    epochs += 1

            self.population = Population.survival_selection(self.population)

            offspring = Population.generate_offspring(self.population)
            self.population.individuals += offspring.individuals

            self.__log(total_generations, epochs, generation)

            total_generations += 1
            generation += 1

        print("Result: {}".format(self.population.fittest.genotype))
        return self.population.fittest


    def __log(self, total_generations, epochs, generation):
        """Log the process of the Evolutionary Algorithm."""
        ...

Although considerably more complicated, this new Evolutionary Algorithm framework allows us to explore much more of a search space (without getting stuck).

Let's put it to the test.

A New 3-SAT Problem

We're going to take on a substantially harder 3-SAT instance: 1,000 clauses, 250 variables. To make it worse, the number of valid solutions is also lower. We will also include the following terminating conditions:

Time of eight hours.
Fitness of all clauses satisfied (100).
A million generations.

So, how does our Evolutionary Algorithm fare?

Not well. After twenty epochs, and thousands of generations — we do not find a solution. Fear not; in subsequent posts, we will work on optimizing our Genetic Algorithm to handle much larger cases, more effectively.

We are going to tackle both of these issues.

Applying Termination Conditions

First, we will examine what criteria we want met before our Evolutionary Algorithm terminates. In general, there are six that are universal:

Date and Time. After a specified date and time, terminate.
Fitness Target. This is what we had before; terminate when any individual attains a certain fitness.
Number of Fitness Evaluations. Every generation, every individual's fitness is evaluated (in our case, every generation $\mu + \lambda$ fitnesses are evaluated). Terminate after a specified number of fitness evaluations.
Number of Generations. Just like the number of fitness evaluations, terminate after a specified generations.
No Change In Average Fitness. This is a bit tricky. After specify $N$ generations, we check every $N$ generations back to determine if the average fitness of a population has improved. We have to be careful in our programming; by preserving diversity, we almost always lose fitness.
No Change In Best Fitness. Just like No Change In Average Fitness, but instead of taking the average fitness, we take the best.

Later, we will see how Conditions 5 & 6 will come in handy to determining if we are stuck in a local optimum.

class _TerminationCondition:
    pass

class FitnessTarget(_TerminationCondition):
    """Terminate after an individual reaches a particular fitness."""

class DateTarget(_TerminationCondition):
    """Terminate after a particular date and time."""

class NoChangeInAverageFitness(_TerminationCondition):
    """Terminate after there has been no change in the average
    fitness for a period of time."""

class NoChangeInBestFitness(_TerminationCondition):
    """Terminate after there has been no change in the best fitness
    for a period of time."""

class NumberOfFitnessEvaluations(_TerminationCondition):
    """Terminate after a particular number of fitness evaluations."""

class NumberOfGenerations(_TerminationCondition):
    """Terminate after a particular number of generations."""

Now, we need something that will keep track of all these conditions, and tells us when we should terminate. And here's where we need to be careful.

First, we need to know when to terminate. We want to mix and match different conditions, depending on the use case. This begs the questions:

Should the Evolutionary Algorithm terminate when one condition has been met, or all of them?

From this, we have everything we might need to keep track of our terminating conditions.

class TerminationManager:
    def __init__(self, termination_conditions, fitness_selector):
        assert isinstance(termination_conditions, list)
        assert all(issubclass(type(condition), _TerminationCondition)
                   for condition in termination_conditions), \
               "Termination condition is not valid"

        self.termination_conditions = termination_conditions
        self.__fitness_selector = fitness_selector

        self.__best_fitnesses = []
        self.__average_fitnesses = []

        self.__number_of_fitness_evaluations = 0
        self.__number_of_generations = 0

    def should_terminate(self):
        for condition in self.termination_conditions:
            if (isinstance(condition, FitnessTarget) and
                    self.__fitness_should_terminate()):
                return True
            elif (isinstance(condition, DateTarget) and
                    self.__date_should_terminate()):
                return True
            elif (isinstance(condition, NoChangeInAverageFitness) and
                    self.__average_fitness_should_terminate()):
                return True
            elif (isinstance(condition, NoChangeInBestFitness) and
                    self.__best_fitness_should_terminate()):
                return True
            elif (isinstance(condition, NumberOfFitnessEvaluations) and
                    self.__fitness_evaluations_should_terminate()):
                return True
            elif (isinstance(condition, NumberOfGenerations) and
                    self.__generations_should_terminate()):
                return True

        return False

    def reset(self):
        """Reset the best fitnesses, average fitnesses, number of
        generations, and number of fitness evaluations."""
        self.__best_fitnesses = []
        self.__average_fitnesses = []

        self.__number_of_fitness_evaluations = 0
        self.__number_of_generations = 0

    def __fitness_should_terminate(self):
        """Determine if should terminate based on the max fitness."""

    def __date_should_terminate(self):
        """Determine if should terminate based on the date."""

    def __average_fitness_should_terminate(self):
        """Determine if should terminate based on the average fitness
        for the last N generations."""

    def __best_fitness_should_terminate(self):
        """Determine if should terminate based on the average fitness
        for the last N generations."""

    def __fitness_evaluations_should_terminate(self):
        """Determine if should terminate based on the number of
        fitness evaluations."""

    def __generations_should_terminate(self):
        """Determine if should terminate based on the number of generations."""

And the changes to our Evolutionary Algorithm are minimal, too.

class EA:
    ...
    
    def search(self, termination_conditions):
        generation = 1
        self.population = Population(self.μ, self.λ)

        fitness_getter = lambda: [individual.fitness
                                  for individual
                                  in self.population.individuals]
        termination_manager = TerminationManager(termination_conditions,
                                                  fitness_getter)

        while not termination_manager.should_terminate():
            offspring = Population.generate_offspring(self.population)
            self.population.individuals += offspring.individuals
            self.population = Population.survival_selection(
                self.population)

            print("Generation #{}: {}".format(
                generation, self.population.fittest.fitness))
            generation += 1

        print("Result: {}".format(self.population.fittest.genotype))
        return self.population.fittest

However, we can still do better.

Generations Into Epochs

How can we determine if we are at a local optimum?

We can't.

Luckily, we already have something that will manage the average/best fitness for us.

class EA:
    ...

    def search(self, termination_conditions):
        epochs, generation, total_generations = 1, 1, 1
        self.population = Population(self.μ, self.λ)

        previous_epoch = []
        fitness_getter = lambda: [individual.fitness
                                  for individual
                                  in self.population.individuals]

        termination_manager = TerminationManager(termination_conditions,
                                                  fitness_getter)
        epoch_manager_best_fitness = TerminationManager(
            [NoChangeInBestFitness(250)], fitness_getter)
        epoch_manager_average_fitness = TerminationManager(
            [NoChangeInAverageFitness(250)], fitness_getter)

        while not termination_manager.should_terminate():
            if (epoch_manager_best_fitness.should_terminate() and
                    epoch_manager_average_fitness.should_terminate()):
                if len(previous_epoch) > 0:
                    epoch_manager_best_fitness.reset()
                    epoch_manager_average_fitness.reset()

                    self.population.individuals += previous_epoch
                    previous_epoch = []
                else:
                    epoch_manager_best_fitness.reset()
                    epoch_manager_average_fitness.reset()

                    previous_epoch = self.population.individuals
                    self.population = Population(self.μ, self.λ)

                    generation = 0
                    epochs += 1

            self.population = Population.survival_selection(self.population)

            offspring = Population.generate_offspring(self.population)
            self.population.individuals += offspring.individuals

            self.__log(total_generations, epochs, generation)

            total_generations += 1
            generation += 1

        print("Result: {}".format(self.population.fittest.genotype))
        return self.population.fittest


    def __log(self, total_generations, epochs, generation):
        """Log the process of the Evolutionary Algorithm."""
        ...

Although considerably more complicated, this new Evolutionary Algorithm framework allows us to explore much more of a search space (without getting stuck).

Let's put it to the test.

A New 3-SAT Problem

Time of eight hours.
Fitness of all clauses satisfied (100).
A million generations.

So, how does our Evolutionary Algorithm fare?

Tuesday, 13 November 2018

, & Illya Starikov

Code, Computer Science

Evolutionary Algorithms Recombination Operators

Permutation, Integer, and Real-Valued Crossover

We have been introduced to recombination operators before; however, that was merely an introduction. There are dozens of different Evolutionary Algorithm recombination operators for any established genotype; some are simple, some are complicated.

For a genotype representation that is a permutation (such as a vector^[1], bit-string, or hash-map^[2]), we have seen a possible recombination operator. Our 3-SAT solver uses a very popular recombination technique: uniform crossover.

Furthermore, we know a permutation is not the only, valid genotype for an individual: other possibilities can include an integer or a real-valued number.

Note, for simplicity, we will discuss recombination to form one offspring. This exact process can be applied to form a second child (generally with the parent's role reversed). Recombination can also be applied to more than two parents (depending on the operator). Again, for simplicity, we choose to omit it^[3].

First, let us start with permutations.

Permutation Crossover

In regard to permutation crossover, there are three common operators:

Uniform Crossover
$N$ -Point Crossover
Davis Crossover

Uniform crossover we have seen before. We consider individual elements in the permutation, and choose one with a random, equal probability. For large enough genotypes, the offspring genotype should consist of 50% of the genotype from parent one, and 50% of the genotype from parent two.

$N$-Point crossover considers segments of a genotype, as opposed to individual elements. This operator splits the genotype of Parent 1 and Parent 2 $N$ times (hence the name $N$-point), and creates a genotype by alternating segments from the two parents. For every $N$, there will be $N + 1$ segments. For 1-point crossover, the genotype should be split into two segments, and the offspring genotype should be composed of one segment from Parent 1, and one segment from Parent 2. For 2-point crossover, there will be three segments, and the offspring genotype will have two parts from Parent 1 and one part from Parent 2 (or two parts, Parent 1, one part, Parent 2).

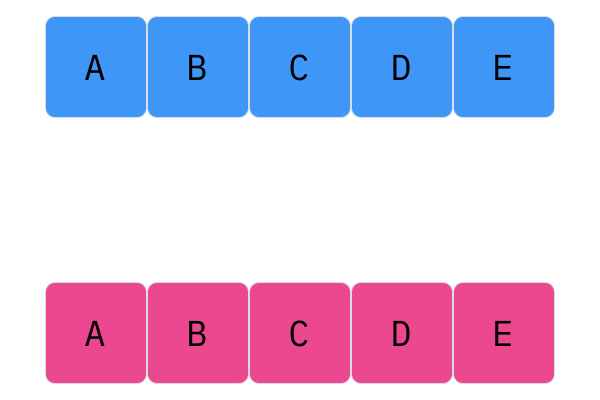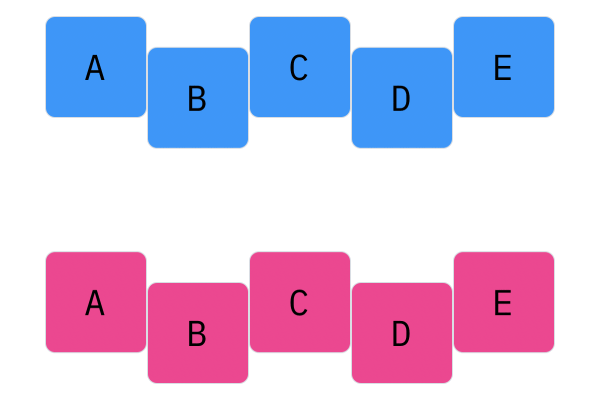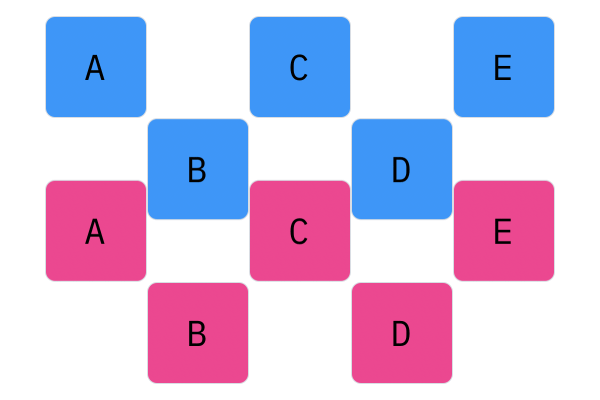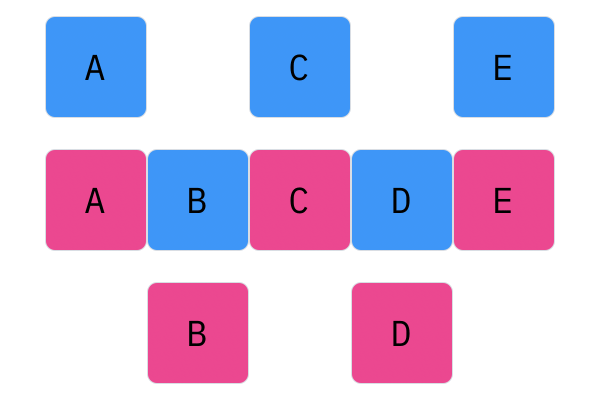
Davis Crossover tries to preserve the ordering of the genotype in the offspring (as opposed to the previous methods, where ordering was not considered). The premise is a bit complicated, but bear with me. Pick two random indices ($k_1$ and $k_2$), and copy the genetic material of Parent 1 from $k_1$ to $k_2$ into the offspring at $k_1$ to $k_2$. Put Parent 1 to the side, his role is finished. Start copying the genotype of Parent 2 starting at $k_1$ to $k_2$ at the beginning of the offspring. When $k_2$ is reached in the parent, start copying the beginning of Parent 2 into the genotype, and when $k_1$ is reached in the parent, skip to $k_2$. When $k_1$ is reached in the offspring, skip to $k_2$, and start copying until the end. If this seems a complicated (it very much is), reference the accompanying figure.

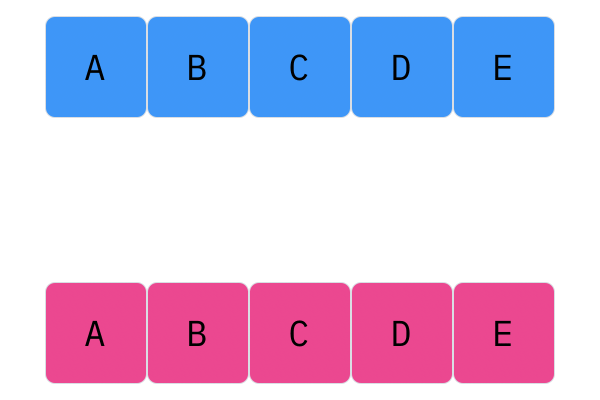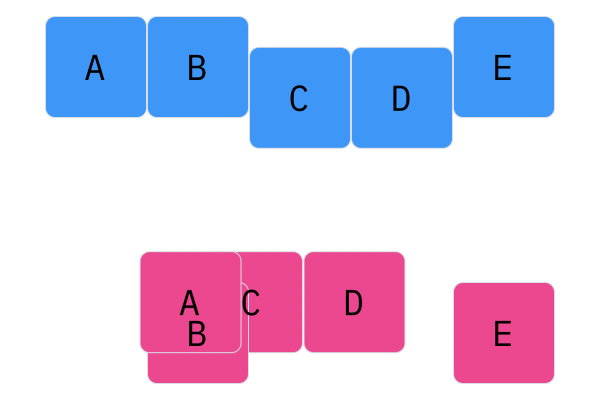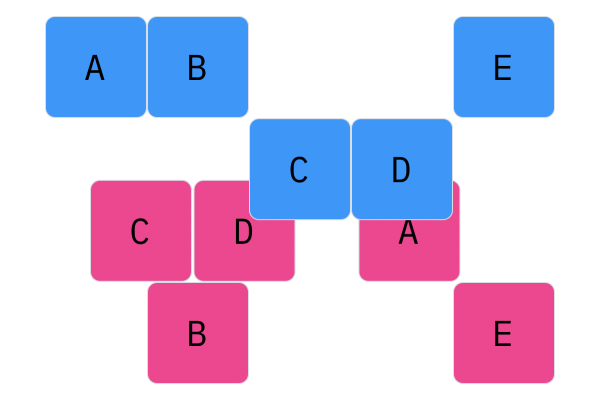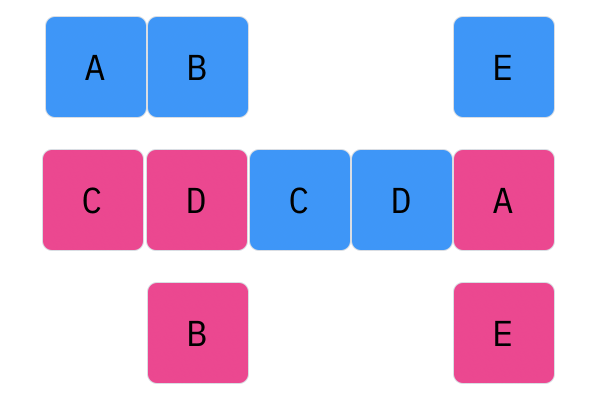
Those are considered the three, most popular choices for permutations. Now, let us look at integer crossover.

Integer Crossover

Integer crossover is actually quite an interesting case; integers can be recombined as permutations or real-valued numbers.

An integer is already a permutation, just not at first glance: binary. The individual bits in a binary string are analogous to elements in a vector, and the whole collection is a vector. Now it is a valid permutation. We can apply uniform crossover, $N$-point crossover, or Davis Crossover, just as we have seen.

An integer is also already a real-valued number, so we can treat it as such. Let's take a look at how to recombine it.

Real-Valued Crossover

Real-Valued crossover is different than methods we have seen before. We could turn it into binary, but that would be a nightmare to deal with. However, we can exploit the arithmetic properties of real-valued numbers — with a weighted, arithmetic mean. For a child (of real value) $z$, we can generate it from Parent 1 $x$ and Parent 2 $y$ as such:

$$
z = \alpha \cdot x + (1 - \alpha) \cdot y
$$

Now, if we want to crossover a permutation of Parent 1 and Parent 2, we can do so for every element.

$$
z_i = \alpha \cdot x_i + (1 - \alpha) \cdot y_i
$$

This can be shown to have better performance than crossover methods discussed, but would entirely depend on use case.

Implementing Permutation Recombination

As always, we will now tackle implementing the permutation crossovers we've had before. None of them are incredibly complicated, except possibly $N$-point crossover.

class Individual
    ...

    @staticmethod
    def __uniform_crossover(parent_one, parent_two):
        new_genotype = SAT(Individual.cnf_filename)

        for variable in parent_one.genotype.variables:
            gene = choice([parent_one.genotype[variable],
                          parent_two.genotype[variable]])
            new_genotype[variable] = gene

        individual = Individual()
        individual.genotype = new_genotype
        return individual

    @staticmethod
    def __n_point_crossover(parent_one, parent_two, n):
        new_genotype = SAT(Individual.cnf_filename)
        variables = sorted(parent_one.genotype.variables)
        splits = [(i * len(variables) // (n + 1)) for i in range(1, n + 2)]

        i = 0
        for index, split in enumerate(splits):
            for variable_index in range(i, split):
                if index % 2 == 0:
                    gene = parent_one.genotype[variables[i]]
                else:
                    gene = parent_two.genotype[variables[i]]
                new_genotype[variables[i]] = gene

                i += 1

        individual = Individual()
        individual.genotype = new_genotype

        return individual

    @staticmethod
    def __davis_crossover(parent_one, parent_two):
        new_genotype = SAT(Individual.cnf_filename)
        variables = sorted(parent_one.genotype.variables)
        split_one, split_two = sorted(sample(range(len(variables)), 2))

        for variable in variables[:split_one]:
            new_genotype[variable] = parent_two.genotype[variable]

        for variable in variables[split_one:split_two]:
            new_genotype[variable] = parent_one.genotype[variable]

        for variable in variables[split_two:]:
            new_genotype[variable] = parent_two.genotype[variable]

        individual = Individual()
        individual.genotype = new_genotype

        return individual

Recombination In General

By no means is recombination easy. It took evolution hundreds of thousands of years to formulate ours. The particular permutation operator to use entirely dependent on the context of the problem; and most of the time, it is not obvious by any stretch. Sometimes, there might not even be an established crossover operator for a particular genotype.

Sometimes, you might have to get a little creative.

List or array in programming terms. ↩︎
Dictionary or map in programming terms. ↩︎
View it as "an exercise left for the reader". ↩︎

Sunday, 11 November 2018

, & Illya Starikov

Code, Computer Science

Steepest-Ascent Hill-Climbing

Search algorithms have a tendency to be complicated. Genetic algorithms have a lot of theory behind them. Adversarial algorithms^[1] have to account for two, conflicting agents. Informed search relies heavily on heuristics. Well, there is one algorithm that is quite easy to grasp right off the bat.

Imagine you are at the bottom of a hill; you have no idea where to go. A decent place to start would be to go up the hill to survey the landscape. Then, restart to find a higher peak until you find the highest peak, right? Well, that is the entire algorithm.

Let's dig a bit deeper.

An Introduction

What is Steepest-Ascent Hill-Climbing, formally? It's nothing more than an agent searching a search space, trying to find a local optimum. It does so by starting out at a random Node, and trying to go uphill at all times.

The pseudocode is rather simple:

current ← Generate-Initial-Node()

while true
    neighbors ← Generate-All-Neighbors(current)
    successor ← Highest-Valued-Node(neighbors)

    if Value-At-Node(successor) <= Value-At-Node(current):
        return current
        
    current ← successor

What is this Value-At-Node and $f$-value mentioned above? It's nothing more than a heuristic value that used as some measure of quality to a given node. Some examples of these are:

Function Maximization: Use the value at the function $f(x, y, \ldots, z)$.
Function Minimization: Same as before, but the reciprocal: $1 / f(x, y, \ldots, z)$.
Path-Finding: Use the reciprocal of the Manhattan distance.
Puzzle-Solving: Use some heuristic to determine how well/close the puzzle is solved.

The best part? If the problem instance can have a heuristic value associated with it, and be able to generate points within the search space, the problem is a candidate for Steepest-Ascent Hill-Climbing.

Implementing Steepest-Ascent Hill-Climbing

For this problem, we are going to solve an intuitive problem: function maximization. Given a function $z = f(x, y)$, for what values of $x, y$ will $z$ be the largest? To start, we are going to use a trivial function to maximize:

$$
z = -x^2 - y^2
$$

We see it is nothing more than a paraboloid. Furthermore, since it is infinite, we are going to restrict the domain to ${ x, y \in \mathbb{Z}^+ : -100 \leq x, y \leq 100 }$; therefore, we only have integer values between $(-100, 100)$.

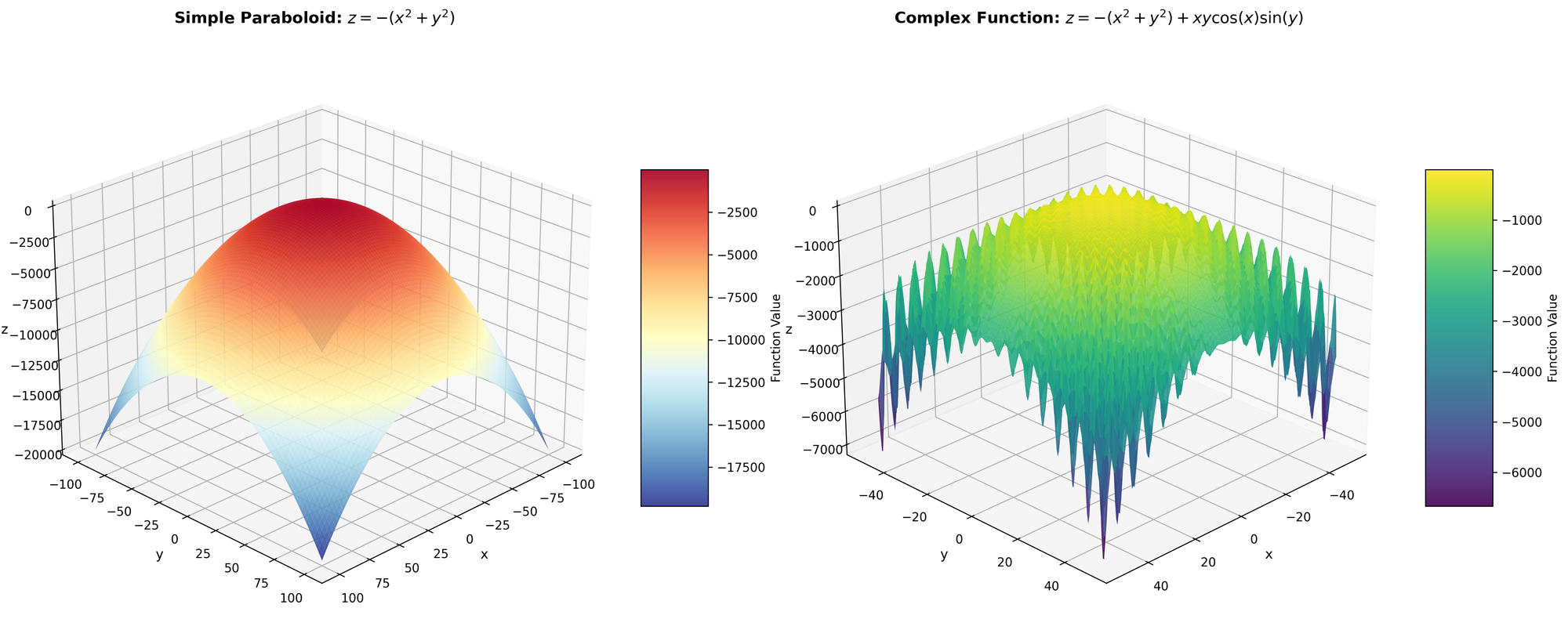
So, let's begin.

The Representation

Because we will be searching throughout a search space, we will need some representation of a state. For our particular problem instance, it's very easy: the points $(x, y)$. Also, we will need to represent the $f$ value, so we create an auxiliary class as well.

class Node:
    """A node in a search space (similar to a point (x, y)."""

    def __init__(self, x, y):
        self.x = x
        self.y = y


class Function:
    """A function and its respective bounds."""

    def __init__(self, function, x_bounds, y_bounds):
        ...

    def __call__(self, node):
        ...

    @property
    def x_bounds(self):
        """Get the x bounds of the function.

        Returns:
            tuple<int, int>: The x bounds of function in the format (min, max).
        """
        ...
        
    @property
    def y_bounds(self):
        """Get the y bounds of the function.

        Returns:
            tuple<int, int>: The y bounds of function in the format (min, max).
        """
        ...

That will be all that we need for our purposes.

Steepest-Ascent Hill-Climbing

As we saw before, there are only four moving pieces that our hill-climbing algorithm has: a way of determining the value at a node, an initial node generator, a neighbor generator, and a way of determining the highest valued neighbor.

Starting with the way of determining the value at a node, it's very intuitive: calculate the value $z = f(x, y)$.

class HillClimber:
    """A steepest-ascent hill-climbing algorithm."""

    def __init__(self, function):
        self.function = function

    def _value_at_node(self, node):
        return self.function(node)

The initial node can simply be taken as a random $(x, y)$ in their respective bounds.

    def _initial_node(self):
        x = randint(self.function.x_bounds[0], self.function.x_bounds[1])
        y = randint(self.function.y_bounds[0], self.function.y_bounds[1])

        return Node(x, y)

Generating neighbors is actually quite simple as well: because our domain is limited to integers, we can simply look at the four cardinal directions (and make sure we won't be breaking the bounds when we do). Also, we randomize the neighbors, to make things more interesting^[2].

    def _generate_all_neighbors(self, node):
        x, y = node.x, node.y

        nodes = [Node(x, y)]

        if x < self.function.x_bounds[1]:
            nodes.append(Node(x + 1, y))
        if x > self.function.x_bounds[0]:
            nodes.append(Node(x - 1, y))
        if y < self.function.y_bounds[1]:
            nodes.append(Node(x, y + 1))
        if y > self.function.y_bounds[0]:
            nodes.append(Node(x, y - 1))

        shuffle(nodes)
        return nodes

Finally, to get the highest value node, it's fairly straightforward:

    def _highest_valued_node(self, neighbors):
        max_point = neighbors[0]

        for point in neighbors[1:]:
            if self._value_at_node(point) > self._value_at_node(max_point):
                max_point = point

        return max_point

Piecing all this together, we get our Steepest-Ascent Hill-Climber:

  def climb(self):
        current_node = self._initial_node()

        while True:
            print("Exploring Node({}, {})".format(current_node.x,
                                                   current_node.y))
            neighbors = self._generate_all_neighbors(current_node)
            successor = self._highest_valued_node(neighbors)

            if (self._value_at_node(successor) <=
                    self._value_at_node(current_node)):
                return current_node

            current_node = successor

Does it work? Exactly as planned.

Exploring Node(5, -88)
...
Exploring Node(5, -67)
...
Exploring Node(5, -47)
...
Exploring Node(5, -27)
...
Exploring Node(5, -4)
Exploring Node(4, -4)
Exploring Node(3, -4)
Exploring Node(3, -3)
Exploring Node(2, -3)
Exploring Node(2, -2)
Exploring Node(1, -2)
Exploring Node(1, -1)
Exploring Node(1, 0)
Exploring Node(0, 0)

However, this was too easy. We had a function with one local optimum. Let's make things interesting.

Optimizing Steepest-Ascent Hill-Climbing

Suppose we keep our previous domain, but we change our function to the following:

$$
z = -(x^2 + y^2) + x\, y\, \cos x \sin y
$$

This function isn't quite as intuitive to visualize, please reference the figure. Essentially, it’s what we had before, but thousands of local optimum when we get further from the center. Our previous Hill-Climbing would absolutely get destroyed by that function.

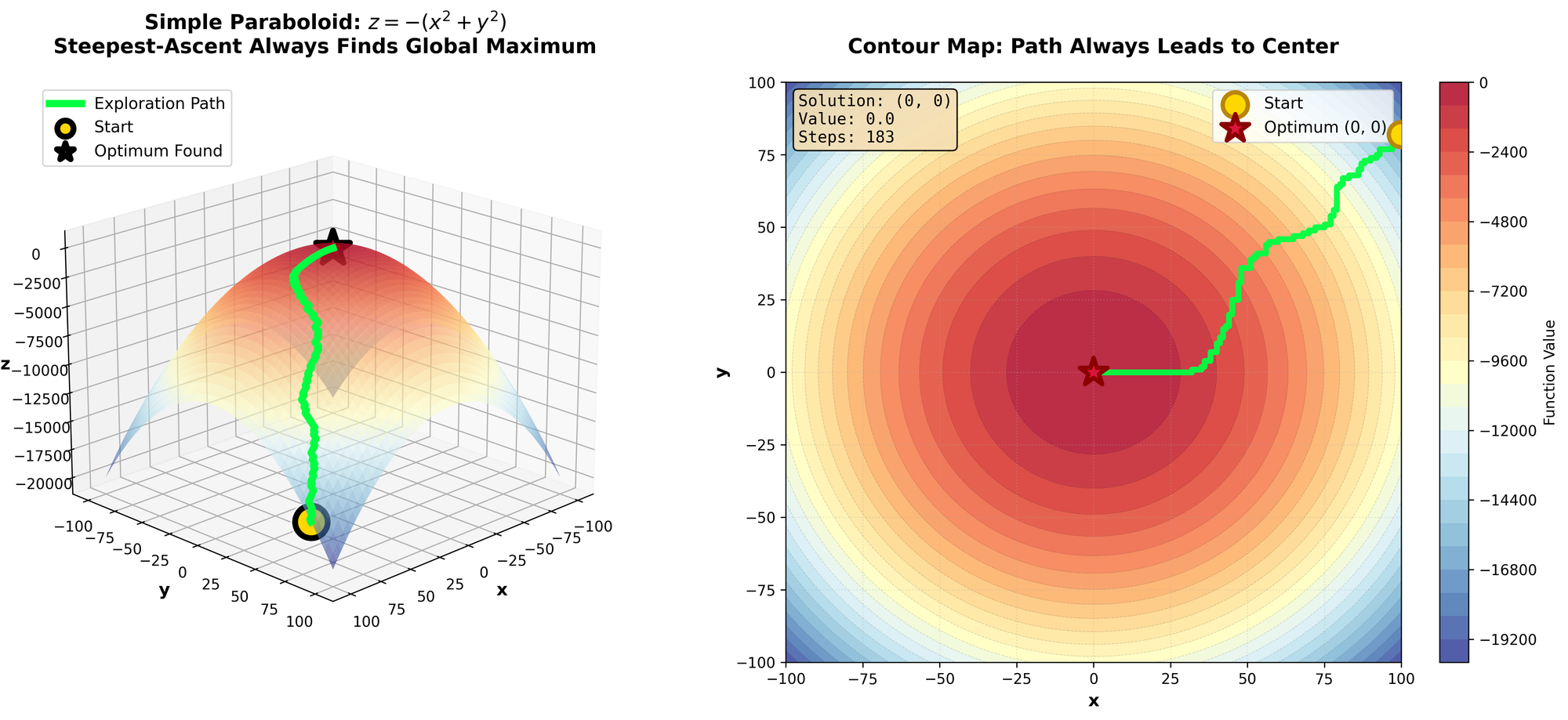
To alleviate this, we are going to use two optimizations:

Instead of taking the steepest uphill move, we are going to simply take a random, uphill move (known as Stochastic Hill-Climbing).
When we get stuck, we are going to restart the search (known as Hill-Climbing With Restarts).

Stochastic Hill-Climbing

Updating the algorithm is fairly simply, all the previous mechanics are inheritable, just swap out _highest_valued_node with a stochastic version.

class StochasticHillClimber(HillClimber):
    """A stochastic steepest-ascent hill-climbing algorithm."""

    def _get_random_uphill_move(self, current_node, neighbors):
        uphill_nodes = []

        for point in neighbors:
            if self._value_at_node(point) > self._value_at_node(current_node):
                uphill_nodes.append(point)

        return current_node if len(uphill_nodes) == 0 else choice(uphill_nodes)

    def climb(self):
        current_node = self._initial_node()

        while True:
            print("Exploring Node({}, {})".format(current_node.x,
                                                   current_node.y))

            neighbors = self._generate_all_neighbors(current_node)
            successor = self._get_random_uphill_move(current_node,
                                                      neighbors)

            if (self._value_at_node(successor) <=
                    self._value_at_node(current_node)):
                return current_node

            current_node = successor

Running this algorithm, we get better results; but we can do better.

Stochastic Hill-Climbing With Restarts

For this, we simply have to restructure the climb function to handle generational effects (like keeping the max valued node throughout generations). Not too difficult.

class StochasticHillClimberWithRestarts(StochasticHillClimber):
    """A stochastic steepest-ascent hill-climbing algorithm with restarts."""

    def climb(self, number_of_generations):
        max_node = self._initial_node()

        for generations in range(number_of_generations):
            current_node = self._initial_node()

            while True:
                msg = "Generation {}, Exploring Node({}, {}), " + \
                      "Current Max Node({}, {})"
                print(msg.format(generations, current_node.x,
                                 current_node.y,
                                 max_node.x, max_node.y))

                neighbors = self._generate_all_neighbors(current_node)
                successor = self._get_random_uphill_move(current_node,
                                                          neighbors)

                if (self._value_at_node(max_node) <
                        self._value_at_node(current_node)):
                    max_node = current_node

                if (self._value_at_node(successor) <=
                        self._value_at_node(current_node)):
                    break

                current_node = successor

        return max_node

How did this one fare? Quite better than all the rest. Let's take a look at what the exploration process looked like.

Marvelous, some got to the top, many got caught in local optimum. A global-optimum was found. A success.

Algorithms used in games, where a player searches for an optimal move against an opponent. ↩︎
If the neighbors are always generated deterministically, there might occur a sequence of ties when generating the highest-valued node. We randomize the neighbors so a random piece will be chosen in the tie-breaker. ↩︎

Friday, 2 November 2018

, & Illya Starikov

Code, Computer Science

The Importance of Parameter Tuning In Evolutionary Algorithms

This is an extension of a blog post I wrote a couple months ago. You can find it here.

One of the big takeaways in my introduction to Evolutionary Algorithms was the sheer number of numerical parameters.

$\mu$ And $\lambda$
Mutation Rate
$k$ in k-Tournament Selection

Not only this, but the sheer number of parameters:

The genotype
The mutator operator
The survivor selection algorithm

And one might be wondering, what is the best operator for $x$ or $y$? Let’s look at an example.

Recall the problem from the previous discussion: We are going to consider a sample problem, a deciphering program. The premise of the problem is as follows:

There is a string of characters (without spaces) hidden away that, after set, is inaccessible.
There are two ways to retrieve data about the hidden message:

1: Get the length of the string.

2: Given a string, the problem will output how many characters match within the two strings.

Disregarding the other technical details, let us focus on the survivor selection. We used $k$ -tournament selection (with $k = 50$). But, let’s run a little experiment:

Run the Evolutionary Algorithm, with $k$ ranging from $5$ (basically the bare minimum) to $100$ ($\lambda$, the population size), and see how fast the algorithm terminates. Do this 1,000 times to get accurate results.

The result?

This makes sense. Our problem has one local optimum: the actual solution. So we do not need a lot of genetic diversity, we need aggressive selective pressure^[1] to reach the top quickly.

As $k$ gets closer to $\mu$, the average termination time decreases. What does this tell us? We picked the wrong survivor selection algorithm.

With $k = \mu$, we no longer have $k$ -tournament selection; we have truncation selection (where only the most fit individuals survive). And that's the interesting part about Evolutionary Algorithms: there are no objective, best parameters.

How do we alleviate this? Trial and error. There is no telling when one parameter is going to perform better than another.

After a couple of trial runs, and objectives in mind (average terminating fitness, best terminating fitness, time to termination), the answer might surprise (and delight) you.

How elitist the survivor selection algorithm is, picking the strongest individuals more often. ↩︎

Wednesday, 3 October 2018

, & Illya Starikov

Code, Computer Science

The Reusability Of Evolutionary Algorithms

3-SAT Solving With EAs

Let's propose an Evolutionary Algorithm experiment; say we already have a framework in place (like the Secret Message framework we previously implemented). How difficult would it be to completely switch problem instances?

First, we need another problem instance. Our previous problem instance was pretty straightforward: it had one local optimum. Let's take on a problem with many local optima, such as the 3-SAT problem.

The premise of 3-SAT is simple. From a global pool of variables ($x_1$, $x_2$, $\ldots$, $x_n$), we have a basic clause of three variables or-ed together (signified by $\vee$):

$$x_p \vee x_q \vee x_r$$

Then, and (signified by a $\wedge$) several clauses together:

$$\left(x_p \vee x_q \vee x_r\right) \wedge \left(x_s \vee x_t \vee x_u\right) \wedge \ldots \wedge \left(x_v \vee x_w \vee x_y\right)$$

The only stipulation is that any variable can be negated (signified by a $\neg$). So, supposing we want to negate $x_p$; $x_s$ and $x_u$; and $x_v$, $x_w$, and $x_y$; we can do the following:

$$\left(\neg x_p \vee x_q \vee x_r\right) \wedge \left(\neg x_s \vee x_t \vee \neg x_u\right) \wedge \ldots \wedge \left(\neg x_v \vee \neg x_w \vee \neg x_y\right)$$

Now, we simply have to assign all the variables such that all the clauses will evaluate to true. It may sound simple, but it belongs to the hardest classes of problems in computer science. There is no guaranteed algorithm to produce the right answer at this time.

For a more visual approach, please reference the figure below. The goal is to make every inner node green, by having at least one connected outer node be green. Note the green nodes have to account for negation as well.

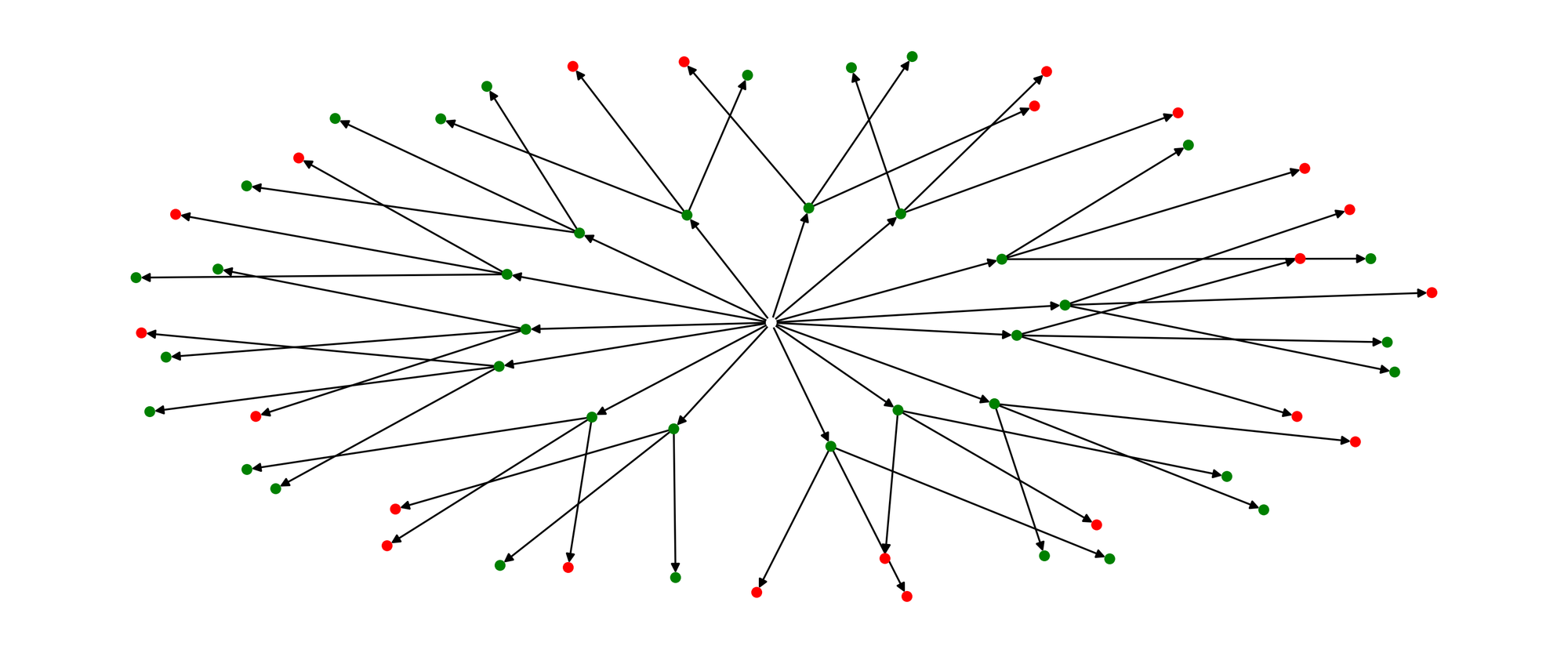
This sounds like a good problem candidate for an Evolutionary Algorithms.

The SAT Problem

We can skip over the problem specific parts to worry more about the Evolutionary Algorithm aspect. Suppose we already have a well-defined SAT class that takes care of SAT-specific properties and methods, like so:

class SAT:
    def __init__(self, filename):
        """Create a SAT object that is read in from a CNF file."""
        ...

    @property
    def variables(self):
        """Get *all* the variables."""
        ...

    @property
    def total_clauses(self):
        """Get the total number of clauses."""
        ...

    @property
    def clauses_satisfied(self):
        """Get the number of satisfied clauses."""
        ...

    def __getitem__(self, key):
        """Get a particular variable (key)"""
        ...

    def __setitem__(self, key, value):
        """Set a variable (key) to value (True/False)"""
        ...

From this, we can create a new genotype for our Individual.

The New Genotype

The genotype structure was very similar to what we had before:

The genotype is the SAT problem we defined above.
Fitness is defined by a percentage of the total satisfied clauses.
Mutation is uniform, choose a percentage $p$ of alleles and flip their value.
Recombination is uniform, randomly assemble values from both parents.

Looking at the refactoring, not much has changed.

The New EA Framework

Now that we have updated our Individual, the next thing to update would be the Evolutionary Algorithm framework, including:

The Population
The EA Itself

Except, we don't have to.

That's the beauty of Evolutionary Algorithms, they are incredibly adaptable. By swapping out the Individual, the rest of the evolutionary algorithm should still work.

For our SAT problem, there were some parameters updated, to make the algorithm more efficient:

The mutation rate has been reduced to 5%
The tournament size has been reduced to 15 individuals (out of $\lambda = 100$).

The Result

So, let's try our Evolutionary Algorithm. Taking a SAT instance with 75 variables and 150 clauses, this makes the search space

$$2^{75} \approx 3.77 \times 10^{22}$$

Great, so roughly 1,000 times the grains of sand on Earth, easy. So, can our EA do it?

After roughly 100 iterations, yes. See the visualization below.

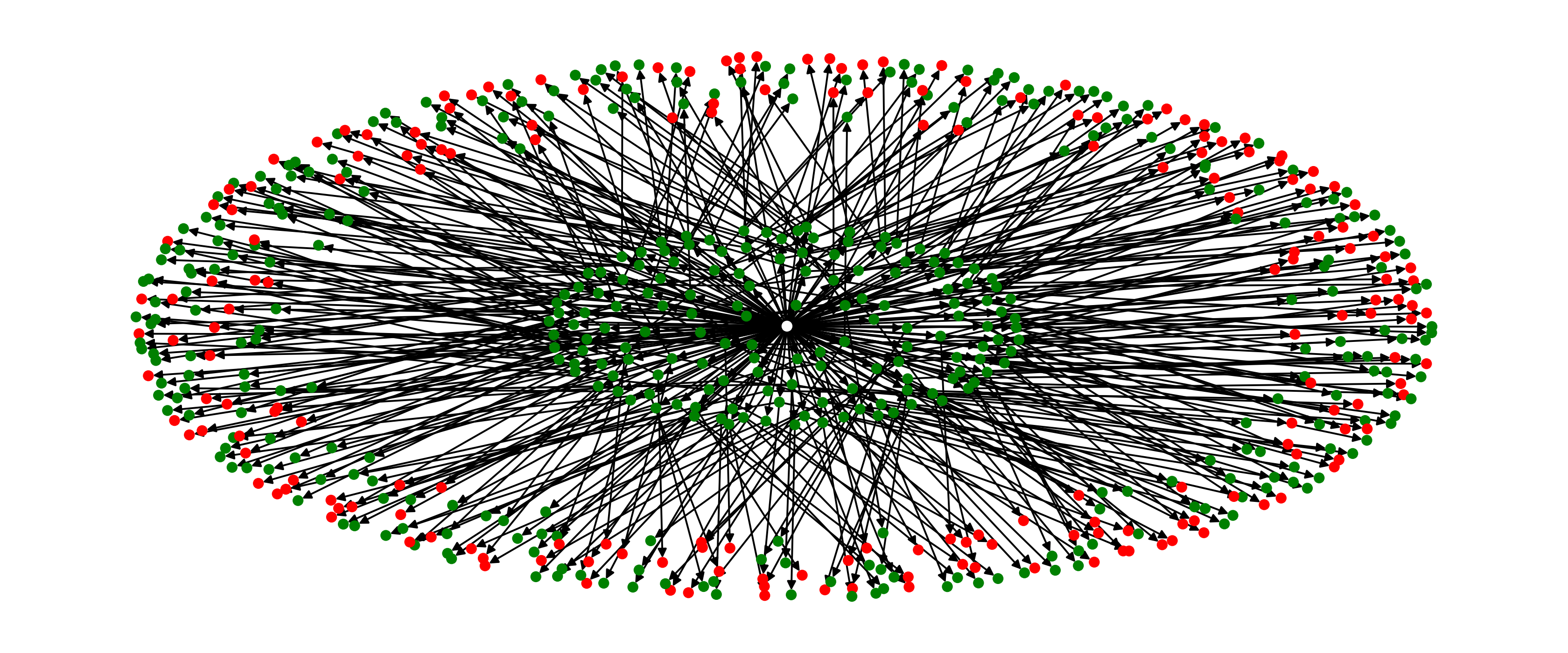
Marvelous, our EA managed to find a solution after only 100 iterations in a giant search space. And all we had to do was swap out one class.

Monday, 1 October 2018

, & Illya Starikov

Code, Computer Science

On Being Passionate About Tools

Get to work. Grab a cup of coffee, some water. Possibly breakfast.

Sit down at my desk. Log into my computer, look at i3wm.

Launch a new terminal session. ranger. Enter. Navigate to project. nvim. Enter.

space f. Use fzf to open necessary file.

This is a daily workflow for me. Before I start typing code, I use about four tools to get to it. Notice, I haven’t mentioned touching the mouse once yet; Because I haven't touched the mouse yet.

Throughout my academic and professional career as a software engineer, I spent a lot of time using tools. Trying new tools. Searching for tools. Customizing tools^[1].

Although this might be a commendable feat, it is often met with skepticism. A lot of skepticism.

I've had at least a hundred conversations with people about tools, about why they advocate against using such tools. These conversations were with other students, senior software engineers, and tenured professors—and generally, almost all of them fell into three distinct buckets of people.

It’s a waste of time.

This is by far the worst yet best counterargument against investing so heavily into tools—and the reasoning is in the trailing three words.

waste. Better tools will objectively help one write more code. If there is a modification that needs to be made at the end of the file, it takes one keystroke to jump to that position in Vim. Picture doing this, but 100s of times a day.

of time. There is a time commitment, a big one. And there is a learning curve, and it is steep. So, one would have to justify the reasons for learning it. And I've done so below.

What I have works just fine.

I’m deeply skeptical of the “If it’s not broken, don’t fix it” mentality. There’s always room for improvement, and there’s nothing more I love to see than improvement.

It’s why we buy new phones. It’s why we like nice, new cars. It’s why we, as civilization, love progress.

Even if it’s a marginal increase, say 5% more code a week. With a 100 lines of code written a week, that can be a about 250 additional lines of code written a year. A marginal increase, sure; but a welcomed one.

It doesn’t really make you a better programmer.

I generally have three core reasons against this, and they are as follows.

It'll help write more code, faster. It is objectively faster to type more code if your hands never leave the keyboard. It's faster to navigate a filesystem without having to focus on where a cursor is. It's ridiculously faster to open a file by just typing out parts of the filename as opposed to navigating to it.

It's healthier. Legitimately. Minimizing hand travel will significantly put less strain on your hands, wrists, and arms.

It'll make you a better programmer. As programmers, we have to learn things all the time. New programming languages, new paradigms, new company software. Learning a new tool keeps a mind sharp by reinforcing how to learn something. Plus, the skills are fluid. Learning to navigate in Vim will help navigate in ranger. Learning regular expressions can be used in fuzzy searches. The skills are transferable.

So, where might one start? Again, there are three areas I see that can have the most benefit from improving your workflow.

Your operating system. Whether it’s Windows, MacOS, or Linux, you have to use an operating system. Get good at it. Learn the paradigms of the system. Learn how the file explorer works in Windows. Learn advanced features in MacOS like a spotlight alternative or simple hot corners. Or learn how to set up your WiFi drivers in Linux.

Your text editor. Choose ones that are portable. I use NeoVim. Many people have success with Emacs. Some people prefer a visual editor like Sublime Text or Atom. Learn their workflows. Learn the shortcuts of Emacs. Learn how to edit text in Normal Mode using Vim. Install packages in Sublime or Atom. You spend most of your time here anyway, might as well get familiar with it.

The intermediary layer between your operating system and your text editor. By this, I usually mean the shell, like Bash or ZSH. Learn how to grep or navigate around. Install packages to make tasks easier. It’s well worth it.

So, yes, I am a strong advocate of using advanced tools. Established tools. Great tools. And I hope I’ve convinced you to do the same.

145 commits worth. ↩︎

Thursday, 27 September 2018

, & Illya Starikov

Computer Science

An Evolutionary Approach To Problem Solving

Arguably the first (and most successful) problem solver we know of is Evolution. Humans (along with other species) all share a common problem: becoming the best at surviving our environment.

Just as Darwinian finches evolved their beaks to survive different parts of the Galápagos Islands, we too evolved to survive different parts of the world. And we can program a computer to do the same.

Evolution inspired a whole generation of problem solving, commonly known as Evolutionary Algorithms (EAs). EAs have been known for solving (or, approximating) solutions to borderline unsolvable problems. And, just as the mechanics of evolution are not that difficult, the mechanics of EAs are just the same.

Today, we will build an Evolutionary Algorithm from the ground-up.

An Introduction

Before we proceed with implementation or an in-depth discussion, first we wish to tackle three questions: what is an Evolutionary Algorithm, what does an Evolutionary Algorithm look like, and what problems can Evolutionary Algorithms solve.

What Is An Evolutionary Algorithm?

An Evolutionary Algorithm is generic, population-based optimization algorithm that generates solution via biological operators. That is quite a mouthful, so let’s break it up.

Population-based. All Evolutionary Algorithms start by creating a population of random individuals. These individuals are just like an individual in nature: there is a genotype (the genes that make up an individual) and a phenotype (the result of the genotype interacting with the environment). In EAs, they would be defined as follows:

Genotype The representation of the solution.
Phenotype The solution itself.

Because it’s a little confusing to think of it this way, it’s often better to think about it in terms of a genotype space and a phenotype space.

Genotype Space The space of all possible combinations of genes.
Phenotype Space The space of all possible solutions.

Don’t worry if this doesn’t make sense, we’ll touch on it later.

Optimization Algorithm. Evolution is an optimization algorithm. Given an environment, it will try to optimize an individual for that environment with some fitness metric. Evolutionary Algorithms operate the same way.

Given an individual, it will try to optimize it. We do not use a literal environment, but still use a fitness metric. The fitness metric is simply a function that takes in the genotype of the individual, and outputs a value that is proportional to how good a solution is.

Because fitness metrics are proportional to how good a solution is, this implies a very important condition for our phenotype space: it’s a gradient.

Biological operators. Evolutionary Algorithms are inspired by biology and evolution. Just as biology has operators to generate new individuals, so do Evolutionary Algorithms. More on that later.

Generic. Evolutionary Algorithms are generic. When a framework has been introduced, it can be reused on an individual basis (provided it has the appropriate crossover and mutator operators).

What Does An Evolutionary Algorithm Look Like?

The pseudocode for an Evolutionary Algorithm is one we might expect evolution to have, generate a random population, generate offspring, and let survival of the fittest do its job. And so it does:

BEGIN
	INITIALISE population with random solutions

	WHILE ( TERMINATION CONDITION is satisfied ) DO
		SELECT parents
		RECOMBINE pairs of parents
		MUTATE the resulting offspring
		EVALUATE new candidates
		SELECT individuals for the next generation
	OD 
END

What Problems Can Evolutionary Algorithms Solve?

Evolutionary Algorithms can solve any problem that has a genotype that can fit within our framework:

The genotype can have a crossover operator.
The genotype can have a mutator operator.
The genotype can map to a definite fitness function.

Again, the fitness should be proportional to how good a solution is. If the fitness function $f(x)$ is bounded by $0 \leq f(x) \leq 100$, 0 should be the worst solution or no solution, and $100$ should be the best solution (or vice versa, for inverted fitnesses).

Implementing An Evolutionary Algorithm

We will be implementing a special class of Evolutionary Algorithm, referred to as a (μ + λ)-Evolutionary Strategy. The name is not important, but μ and λ will be; we will come back to them shortly.

For the purposes of our discussion, we are going to consider a sample problem: a deciphering program. The premise of the problem is such.

There is a string of characters (without spaces) hidden away that, after set, is inaccessible.
There are two ways to retrieve data about the hidden message:
1. Get the length of the string.
2. Given a string, the problem will output how many characters match within the two strings.

The secret message would look as follows:

class SecretMessage:
	def __init__(self, message):
		"""Initialize a Secret Message object.

		:message (str): The secret message to hide.
		"""
		self.__message = message

	def letters_match(self, message):
		"""Determine how many characters match the secret message.

		Note:
			The message length and the secret message length must be
			the same length (accessed via the length property).


		:message (str): The message to compare the secret message to.
		:returns (int): The number of characters matched.
		"""
		return sum(self.__message[char] == message[char]
		           for char in range(len(message)))

	@property
	def length(self):
		"""Get the length of the secret message.

		:returns (int): The length of the secret message.
		"""
		return len(self.__message)

Not too complicated.

An Individual

In Evolutionary Algorithms, an individual is simply a candidate solution. An individual has a genotype (the representation) and operators (Crossover, Mutation, and Fitness) that act on the genotype. We will discuss them more extensively below.

The Genotype

As aforementioned, a genotype is the representation of an individual. Just as DNA does for humans, knowing the genotype can give you all the information one might need to determine the characteristics of an individual.

Because a genotype must be acted upon a crossover and mutation operator, there are few common choices for genotypes:

Vectors^[1]. A vector is common because crossover is trivial, take elements from the two genotypes to create a new individual. Mutation is also trivial, pick random elements in vector, and mutate them. Often, for a complex enough individual, a vector of bits is used^[2].
Matrices. Same as a vector, but with multiple dimensions.
Float-Point or Real Numbers. This one is tricky, but commonly used. There are a plethora of ways to recombine two numbers: average of the two numbers, bit manipulation, binary encoding crossover. Same can be said for mutation: adding a random value to the number, bit manipulation with a random value, or bit flipping in binary encoding. It should be noted that some of these introduce biases, and one should account for them.
Trees. Some problems can be easily broken down into trees (like an entire programming language can be broken down into a parse tree). Crossover is trivial, swap a random subtree with another. Mutation, however, is often not used; this is because the crossover itself acts as a mutation operator.

Next, our genotype must be initialized to some random values. Our initial population is seeded with said randomly-generated individuals, and with a good distribution, they will cover a large portion of the genotype space.

Keeping all this in mind, let us think about the representation of our problem. A string is nothing more than a vector of characters, so using the first bullet point, we are given our operators pretty easily.

Here’s what our genotype would look like:

class Individual:
	message = SecretMessage("")

	def __init__(self):
		"""Initialize an Individual object.

		Note:
			Individual.message should be initialized first.
		"""
		length = Individual.message.length
		characters = [choice(ascii_letters) for _ in range(length)]
		self.genotype = "".join(characters)

Crossover, Mutation, and Fitness

As aforementioned, to fit within an Evolutionary Algorithm framework, a genotype must be created with crossover, mutator, and fitness operators. Although we have covered said operators, we will formalize them here.

Crossover. A crossover operator simply takes in two genotypes, and produces a genotype that is a mixture of the two. The crossover can be uniform (random elements from both genotypes are taken), 1-point (take a pivot position between two points, the left half is one genotype, and the right half another), and $N$-point (same as 1-point but with multiple pivot positions).
Mutator. A mutator operator takes random values within the genotype and changes them to a random values. There is a mutation rate that is associated with all genotypes, we call it $p$. $p$ is bounded such that $0 \leq p \leq 1.0$, where $p$ is the percentage of the genotype that gets mutated. Careful to limit this value, however; too high $p$ can result in just a random search.
Fitness. The fitness operator simply takes in a genotype, and outputs a numerical value proportional to how good a candidate solution is. Fitness has no limits, and can be inverted (i.e., a smaller fitness is better).

For the purposes of our program, we are going to have the following operators: crossover will be uniform, mutation will be a fixed number of mutating characters, and fitness will be a percentage of the characters matched.

class Individual
	...
	@property
	def fitness(self):
		"""Get the fitness of an individual. This is done via a
		percentage of how many characters in the genotype match the
		actual message.

		:return (float): The fitness of an individual.
		"""
		matches = Individual.message.letters_match(self.genotype)
		return 100 * matches / Individual.message.length

	@staticmethod
	def mutate(individual, rate):
		"""Mutation operator --- mutate an individual with a
		specified rate. This is done via a uniform random mutation,
		by selecting random genes and swapping them.

		Note:
			rate should be a floating point number (0.0 < rate < 1.0).

		:individual (Individual): The individual to mutate.
		:rate (float): The rate at which to mutate the genotype.
		"""
		num_to_mutate = int(rate * individual.message.length)
		# Strings are immutable, we have to use a list
		genotype_list = list(individual.genotype)

		for _ in range(num_to_mutate):
			char_to_mutate = choice(range(individual.message.length))
			genotype_list[char_to_mutate] = choice(ascii_letters)

		individual.genotype = "".join(genotype_list)

	@staticmethod
	def recombine(parent_one, parent_two):
		"""Recombination operator --- combine two individuals to
		generate an offspring.

		:parent_one (Individual): The first parent.
		:parent_two (Individual): The second parent.
		:returns (Individual): The combination of the two parents.
		"""
		new_genotype = ""

		for gene_one, gene_two in zip(parent_one.genotype, parent_two.genotype):
			gene = choice([gene_one, gene_two])
			new_genotype += gene

		individual = Individual()
		individual.genotype = new_genotype
		return individual

A Population

Now that we have an Individual, we must create a Population. The Population holds the candidate solutions, creates new offspring, and determine which are to propagate into further generations.

μ And λ

Remember when we mentioned that μ and λ would be important in our Evolutionary Algorithm? Well, now here they come into play. μ And λ are defined as follows:

μ: The population size.
λ: The number of offspring to create.

Although these are simple constants, they can have a drastic impact on an Evolutionary Algorithm. For example, a Population size of 1,000 might find a solution in much fewer generations than 100, but will take longer to process. It has been experimentally shown that a good proportion between the two is:

$$
λ / μ \approx 6
$$

However, this is tested for a large class of problems, and a particular Evolutionary Algorithm could benefit from having different proportions.

For our purposes, we will pick $μ = 100$ and $λ = 15$, a proportion just a little over 6.

class Population:
	def __init__(self, μ, λ):
		"""Initialize a population of individuals.

		:μ (int): The population size.
		:λ (int): The offspring size.
		"""
		self.μ, self.λ = μ, λ

		self.individuals = [Individual() for _ in range(self.μ)]

Generating Offspring

Generating offspring is trivial with the framework we imposed on an Individual: pick two random parents, perform a crossover between the two to create a child, mutate said child, and introduce the child back into the population pool.

In code, it would look as follows:

class Population:
	...

	@staticmethod
	def random_parents(population):
		"""Get two random parents from a population.

		:return (Individual, Individual): Two random parents.

		"""
		msg_len = population.individuals[0].message.length
		split = choice(range(1, msg_len))
		parent_one = choice(population.individuals[:split])
		parent_two = choice(population.individuals[split:])
		return parent_one, parent_two

	@staticmethod
	def generate_offspring(population):
		"""Generate offspring from a Population by picking two random
		parents, recombining them, mutating the child, and adding it
		to the offspring. The number of offspring is determined by λ.

		:population (Population): The population to generate from.
		:returns (Population): The offspring (of size λ).
		"""
		offspring = Population(population.μ, population.λ)
		offspring.individuals = []

		for _ in range(population.λ):
			parent_one, parent_two = Population.random_parents(population)

			child = Individual.recombine(parent_one, parent_two)
			child.mutate(child, 0.15)

			offspring.individuals += [child]

		return offspring

Survivor Selection

The last core part of an Evolutionary Algorithm would be survival selection. This puts selective pressure on our candidate solutions, and what ultimately leads to fitter solutions.

Survivor selection picks μ Individuals that would be the best to propagate into the next generation; however, it’s not as easy as picking the fittest μ Individuals. Always picking the μ best Individuals leads to premature convergence, a way of saying we “got a good solution, but not the best solution”. The Evolutionary Algorithm simply did not explore the search space enough to find other, fitter solutions.

There are a number of ways to run a survival selection, one of the most popular being $k$ -tournament selection. $k$ -tournament selection picks $k$ random Individuals from the pool, and selects the fittest Individual from the tournament. It does this μ times, to get the full, new Population. The higher $k$, the higher the selective pressure; however, also the higher chance of premature convergence. The lower $k$, the less of a chance of premature convergence, but also the more the Evolutionary Algorithm starts just randomly searching.

At the bounds, $k = 1$ will always be just a random search, and $k = μ$ will always be choosing the best μ individuals.

We choose $k = 25$, giving less fit solutions a chance to win, but still focusing on the more fit solutions.

@staticmethod
	def survival_selection(population):
		"""Determine from the population what individuals should not
		be killed. This is done via k-tournament selection: generate
		a tournament of k random individuals, pick the fittest
		individuals, add it to survivors, and remove it from the
		original population.

		Note:
			The population should be of size μ + λ.
			The resultant population will be of size μ.

		:population (Population): The population to run survival
		                          selection on. Must be of size μ + λ.
		:returns (Population): The resultant population after killing
		                       off unfit individuals. Will be of size μ.
		"""
		new_population = Population(population.μ, population.λ)
		new_population.individuals = []

		individuals = deepcopy(population.individuals)

		for _ in range(population.μ):
			tournament = sample(individuals, 25)
			victor = max(tournament, key=lambda individual: individual.fitness)

			new_population.individuals += [victor]
			individuals.remove(victor)

		return new_population

The Evolutionary Algorithm

As with the pseudocode in the introduction, this will exactly resemble our Evolutionary Algorithm. Because the Individual and the Population framework is established, it is almost a copy-paste.

class EA:
	def __init__(self, μ, λ):
		"""Initialize an EA.

		:μ (int): The population size.
		:λ (int): The offspring size.
		"""
		self.μ, self.λ = μ, λ
		
	def search(self):
		"""Run the genetic algorithm until the fitness reaches 100%.

		:returns: The fittest individual.
		"""
		generation = 1
		self.population = Population(self.μ, self.λ)

		while self.population.fittest.fitness < 100.0:
			offspring = Population.generate_offspring(self.population)
			self.population.individuals += offspring.individuals
			self.population = Population.survival_selection(self.population)

			generation += 1

Running An Evolutionary Algorithm

Below, we have an instance of the evolutionary algorithm searching for a solution:

Now, looking at the string “FreneticArray”, it has 13 characters, and seeing as there are 26 letters in the alphabet, double that for lowercase/uppercase letters, our search space was:

$$
\left(2 * 26\right)^{13} \approx 2.0 \times 10^{22}
$$

Huge.

On average, our EA took 29 generations to finish^[3]. As each generation had at most 115 individuals, we can conclude on average we had to generate:

$$
29 * 115 = 3335\, \text{solutions}
$$

Much smaller than $2.0 \times 10^{22}$. That is what Evolutionary Algorithms are good for: turning a large search space into a much smaller one.

Although there are much more advanced topics in Evolutionary Algorithms, this is enough start implementing your own. With just the simple operators listed above, a genotype, a search space that has a gradient, many problems can solved with an Evolutionary Algorithm.

A mathematical vector, common to linear algebra. Just a collection of related items, often referred to as an array in computer science. ↩︎
Hey, if it’s powerful enough to run modern computers, surely it can be adequate enough for a genotype representation. ↩︎
Per 1,000 runs. ↩︎

Wednesday, 12 September 2018

, & Illya Starikov

Code, Computer Science